結果から8節点ヘキサ1次要素を使う場合は、低減精度積分が必要になってきます。今回用いた低減精度積分は全ての積分項 に適用しましたが、せん断応力項のみに適用するともっと面白い結果が出てくると思います。支配方程式からみると、 Gが付く項(垂直応力およびせん断応力)とλ(膨張収縮応力)が付く項は、別々の積分テクニックで積分する必要がありそうです。 多分、垂直応力とせん断応力の項を区別して積分ルールを適用する必要はなさそうです。ためしてみてください。
■3次元主応力の計算■
全てのせん断応力がゼロになる条件下での法線応力を主応力(Principal Stresses)と呼びτ1, τ2, τ3で表します 。
全てのせん断応力をゼロにするには座標軸を回転しなければなりません。
ここでは、主応力をτiで、τiの方向を示す座標軸のベクトルをa=axi+ ayj+ azk で表すと下式のように書けます。
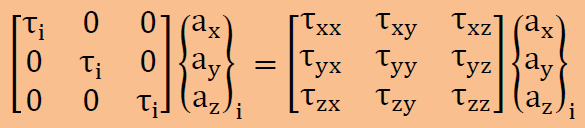
上式のベクトルは、Directional cosine(方向余弦)とも呼ばれていて次の特徴を持っています。
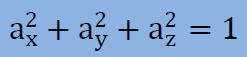
上のマトリクス式は、以下のようにも書けます。ここで、下のマトリクスを[M]と呼ぶことにします。
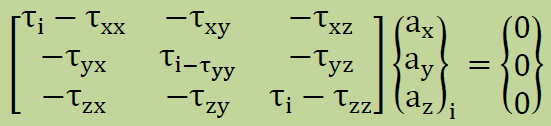
ベクトルは、ゼロになりえないため、上のマトリクス式が成り立つためには、マトリクスの行列式(determinant)がゼロでなければなりません。 つまりこれは固有値問題と同じになります。 したがって固有値と固有ベクトルを計算出来る方法を使えば主応力と座標回転角度は簡単に得ることができます。 実際に POST3DTAUX.FOR ではJacobi法で主応力とベクトルを計算しています。確認のために、ここでは様々な方法で主応力とベクトルを計算するプログラムを作成しました。 参考にして下さい。プログラム名は PSST.FORと PRINCIPALSTRESS.FOR です。これらのプログラムには、Jacobi法以外にNewton-Raphson法、3次方程式を直接解くCardano法、Power法、Bisection法が盛り込まれています。プログラムPRINCIPALSTRESS.FORは、POST3DTAUX.FORが吐き出した応力を読み込みます。PSST.FORは、1ケースのτijに対し主応力とベクトルを計算してくれます。
■3次方程式解法Cardano法による主応力の解法■
上のマトリクスの行列式を計算すると、次の3次式が得られます。主応力の計算に限って、3次式の根は全て実根であることが証明されています。
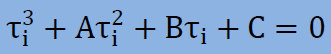
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |