といった感じで展開できます。Sturm列P_i(λ)は[T]のi行i列までの部分の行列式になっているということが解ります。 従って、P_n(λ)＝|[T]|ですからP_n(λ)の根を全て割り出すと、それらの値は固有値ということになります。 上の式を観察すると、P_i(λ)はP₀(λ)からP_i-1(λ)の要素を含み、P_i-1(λ)より1つ次数が多いことになります。 従って、λの値を変えたときP_n-1(λ)とP_n(λ)間で符号が変われば、そのλは固有値に近い値ということになります。 このλが何個目の固有値かを調べるには、P_n(λ)をグラフに描き符号が何回反転(またはゼロを通過する回数) したかを数えれば解ります。しかし、それは大変な作業です。ところが、この符号の反転回数は、 P₁(λ)からP_n(λ)までの符号の反転回数と同じになることが知られています。 Sturmの定理によると、任意に決めた値λに対しSturm列の符号が反転する回数N(λ)をカウントすると、 λより小さい固有値がN(λ)個存在するとあります。 更に、全ての固有値は、[‐b, b]の範囲に存在することが知られている。この値bは以下の式で与えられています。

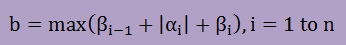
詳しいことは、文献を調査してみて下さい。

Bisection法の計算手順としては、以下のようになります。
(1) 固有値を計算したい[T]行列のサイズをnとします。
(2) Sturm列の符号が反転する回数がmode=1からnになる固有値を順次探します。
(3) 固有値の下限値を a₁=‐bとします。
(4) 固有値の上限値を a₂=bとします。
(5) 固有値の存在範囲(a₂−a₁)/bが誤差判定εより小さいときは、(9)へ移動する。誤差判定εは、倍精度の場合、ε=1×10^-13前後が適切と思います。
(6) Sturm列の符号が反転する回数がmodeになる固有値の近似として以下で予測します。上下限値の中間点をとるということからBisectionと呼ばれています。

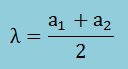
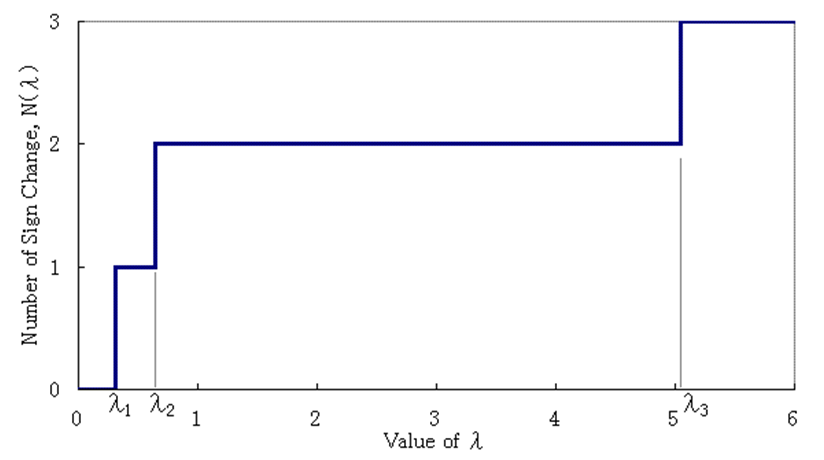
(7) Sturm列を計算しN(λ)を割り出す。以下は、例題の行列[A]を[T]に変換し、 P₀(λ)からP₃(λ)までの間で反転した回数です。 横軸は、任意に決めたλです。反転数が変化した位置のλが固有値になります。