初期ベクトル{u}1は[A]の対角要素で生成してみました。以下がそうです。数字の385は、102+92+…………+12の結果です。つまりベクトルの長さの二乗です。
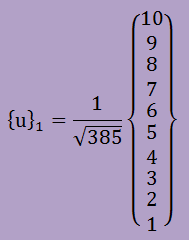
計算に使ったプログラムは、LANCZOS_PRINCIPLE3.FORです。 マトリクス[A]のサイズはこれまで通りNで表し、求めたい固有値の数またはマトリクス[T]のサイズはNLANCZOSで表してあります。 プログラミング的には、LANCZOS_PRINCIPLE2.FORと殆ど同じで、[T]を生成 するときの繰り返し演算の最終値がNからNLANCZOSに変わっているだけです。
まず、m=2(NLANCZOS=2)で計算してみます。固有値の計算は、Bisection法、Jacobi法、Power法で計算し、 全てが同じ値であることを確認しています。値は、以下のようになりました。
| Mode | Eigenvalue |
|---|---|
| 1 | 44.765486656275506 |
| 2 | 4.456735565946723 |
固有値λ1は厳密解とほぼ一致していますが、λ2は誤差が大きいようです。
次にm=3(NLANCZOS=3)で計算してみましょう。以下が結果です。
| Mode | Eigenvalue |
|---|---|
| 1 | 44.76606854162057 |
| 2 | 5.033995231937602 |
| 3 | 1.430705457211068 |
固有値λ1はかなり精度が上がってきました。そして、λ2も精度が向上してきています。しかし、λ3は誤差が大きいです。最後に、m=4(NLANCZOS=4)で計算してみましょう。以下が結果です。
| Mode | Eigenvalue |
|---|---|
| 1 | 44.7660686527091 |
| 2 | 5.048824708377716 |
| 3 | 1.838007510320153 |
| 4 | 0.700040305063633 |
以上の結果から解ることは、最大固有値の精度が一番高く、固有値が小さくなるほど精度が落ちてきます。 例えばm=4の場合、最大固有値λ1は厳密解に近いが、λ4はかなり誤差が大きいですよね。 最大固有値に収束するというKrylov列が関係しているからです。
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |