ここで、以下を再定義します。
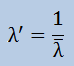
すると最終的に解く固有値問題は、以下になります。
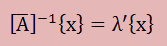
やっと、固有値問題の形式になりました。ここまで来るとこれまでに学習したさまざまな固有値の計算方法が 使えます。そして、最大固有値λ'は、最小の固有値λに対応することになります。 設計に必要な固有値が一番先に計算されることになります。 つまり、上式にLanczos法を適用し部分空間での[T]を生成し固有値λ'を計算できれば、 以下の式で実空間の固有値λを得ることができます。
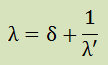
また、[T]の対角要素のαとβを生成するためには、
[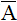 ]-1{u}i
を計算しなければなりません。大きな行列の逆行列を計算するのは、不可能に近くまた計算できたとしても
計算時間が膨大になってしまいます。そこで、以下のように定義します。
]-1{u}i
を計算しなければなりません。大きな行列の逆行列を計算するのは、不可能に近くまた計算できたとしても
計算時間が膨大になってしまいます。そこで、以下のように定義します。
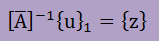
ということは、以下の連立方程式を解くのと同じになります。
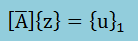
ここまでをプログラムにしてみました。 プログラムの名称は、LANCZOS_PRINCIPLE5.FORです。実際に上の 連立方程式を解いてαを計算し、再直交後βと次の{u}2を計算しています。{u}NLANCZOSが 得られるまで計算を続けます。そして全てのαとβより[T]が生成されると、固有値と固有ベクトル が計算されます。Bisection法ではαとβより直接的に固有値を求めています。計算例は後で紹介します。
■Shifted-Invert Lanczos/LU Decomposition■
固有値計算では、上式を固有値の数だけの回数の計算が必要になります。そこで、
行列[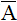 ]を以下で説明するLUで分解しておきます。
]を以下で説明するLUで分解しておきます。
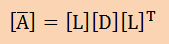
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |