グラフにすると以下になります。縦軸がRで横軸がNEX数です。
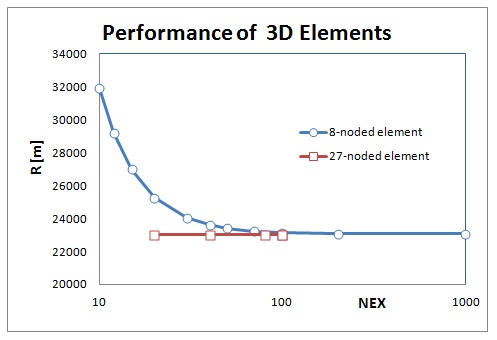
計算結果を見ると、27節点ヘキサ2次要素は素晴らしいパフォーマンスを見せてくれています。つまり、Shear Locking は起きていないと考えて良いでしょう。しかし、8節点ヘキサ1次要素では要素数を増やしていってもShear Lockingにより Rが収束解の22997.3mより小さくなることはありません。つまり、部材がちょっと硬めになった計算結果をだしています。 これは積分点の位置(ξ= +/-0.577350)の都合により要素間の剛性が数値的に高くなっているからです。
そこで、計算結果が収束解のR=22997.3m(厳密解=23000m)になるように Free selection 2点法(フル積分の低減精度積分法-2次元を参考) で積分のサンプリング点の位置を変えながら計算してみました。このFree selection 2点法は全ての積分項に適用します。 すると、NEX=100の場合ξ=0.4880でRが収束解と一致します。同様にその他の要素分割数でも計算を実施しました。結果は、下表の通りです。
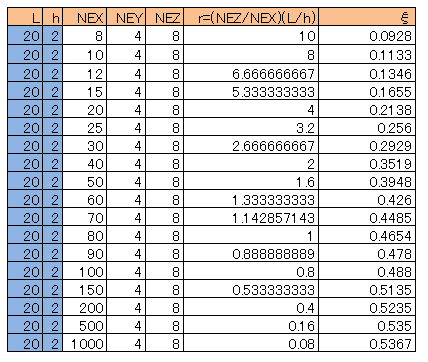
上の表を見ると、無次元数値rが大きいときにはξの値は小さく、rが小さいときにはξの値を大きくする必要が有ります。 3次元の場合、無次元数値rは以下のように定義しました。つまり、無次元数値rは要素のアスペクト比と同じです。 大きいアスペクト比(長い要素)の要素では、積分点を要素の中央寄りにして(ξの値を小さく)、要素間の数値的な剛性を弱くする必要が有ります。 アスペクト比が小さい要素であっても、Gauss-Legendre2点法(ξ= +/-0.577350)では、 要素間の数値剛性が強いので、ξ= +/-0.5216から上表のξ= +/-0.5367以下に設定しなければなりません。
| r=(NEZ/NEX)(L/h)=ΔX/ΔZ |
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |