すると、積分は以下の式で書けます。

Gauss-Legendre 2点法では、ξ1=-ξ, ξ2=+ξ, w1=w2=wとすると、ξ=√(1/3)=0.57735 , w=1になっています。重み係数wが対称になっているのは、f(ξ)=一定も積分できるようになっているからです。それから、ξ=√(1/3)とするとf(ξ)が3次関数まで厳密に積分できます。しかし、計算精度を気にしなければ、ξの選択として0から1が考えられます。つまり、ξ=1とすると台形公式(Trapezoidal rule)になり、ξ=ゼロではGauss-Legendre 1点法(矩形公式とも言う)になります。むろん、ξとして0, 1, 0.57735以外の数値を選択することができます。便宜上、ξに0から1の間を選択することをここでは、Free selection法と呼ぶことにしておきます。 ここで読者に知っておいてもらいたいことは、ξに0から1のいかなる値を選択しようが、関数f(ξ)が線形だと積分結果は厳密解が得られます。表計算ソフトを使って確認しておいて下さい。下に積分点数として2を選んだ場合の積分式の名称を示します。
| ξ | 積分方法の名前 |
|---|---|
| 1 | 台形公式(Trapezoidal rule) |
| 0.999〜0.5774 | 名前無し |
| 0.577350269 | Gauss-Regendre 2点法 |
| 0.5773〜0.0001 | 名前無し |
| 0 | 矩形公式(Gauss-Regendre 1点法) |
積分点数として3を選んだ場合、2次関数の積分が厳密に得られるように積分点ξと重み係数wを計算すると以下が得られます。
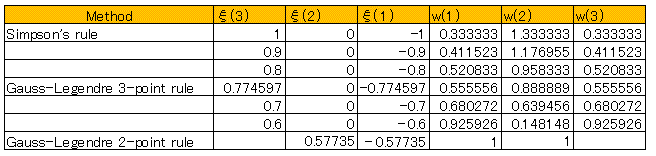
ここに、積分点ξが与えられると重み係数は、w2=(2/3)(3-1/ξ32), w1=w3=(2-w2)/2で得られます。
ちょっと脱線しましたが、早速、Free selection 2点法で4-noded Iso-parametric要素のプログラムを実行してみます。下図が計算結果になります。NEX=100で固定してNEYを4から20まで、そしてξを0.6から0.5までで計算してあります。グラフの縦軸は収束解のRと比較したときの誤差、横軸が縦方向の分割数(NEY)です。9節点要素による計算結果も以下のグラフにプロットしてあります。
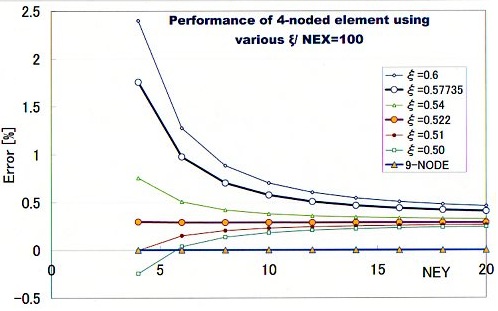
積分点ξをGauss-Legendreの位置よりξ=0の方向へ移動すると、計算誤差は小さくなっています。そして、ξ=0.522を選択すると縦方向の分割数(NEY)に関係なく安定した解が得られています。また、積分点を適切に選択すると、収束解のRと同値を計算させることが可能になります。例えば、NEY=4の場合ξ=0.51で、NEY=6の場合ξ=0.50で誤差がゼロになります。 今度は、要素分割をNEY×NEX=10×100に固定し、ξを1から0までふってみました。この場合、全ての要素のアスペクト比(縦と横の比率)が1に成ります。すると、下図の計算結果が得られました。グラフの縦軸がRの%誤差で横軸がξです。グラフをみるとξ=0.46で誤差がほぼゼロになっています。アスペクト比が1のときξ=0.46が最適値ということが言えます。

| BACK | NEXT |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |