すると改善された主応力は以下で計算できます。

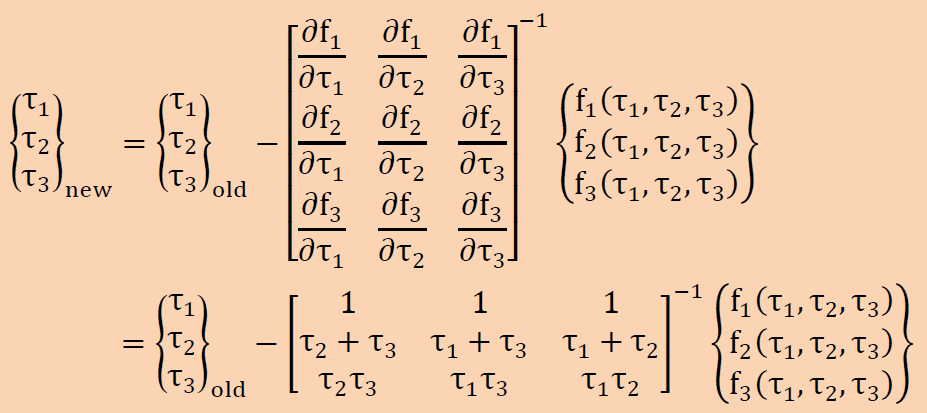
上の式を繰り返すことにより、計算値は真の値に近づきます。 繰り返し計算の数を減らすには、できるだけ真に近い主応力の初期値が必要になります。ここでは、以下の値を使っています。 ここで注意しなければならないことは、マトリクス[D]の行列式がゼロにならないことです。τ₁=τ₂=τ₃だと行列式がゼロになります。つまり、主応力が三重根に収束する場合、この方法は発散することになります。ですから、三重根にならないことを確認してから計算を開始しなければなりません。ちなみにマトリクス[D]の行列式は τ₁τ₂(τ₁-τ₂)+ τ₂τ₃(τ₂-τ₃)+ τ₃τ₁(τ₃-τ₁)です。

計算が収束したかどうかは、以下のエネルギー差で判断しています。

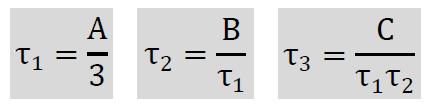
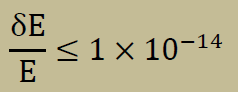
計算結果をみると、4から10回程度で収束しています。しかし、応力の値が非常に小さい場合、繰り返し計算数が増える場合があります。

■その他の方法■
Jacobi法のように固有値と固有ベクトルが同時に計算できる方法としてPower法があります。この方法を使う場合、最初に計算される主応力が負の値にならないように、法線応力(τ_xx,τ_yy,τ_zz)にバイアス応力を加算しておく必要があります。Power法では、計算の過程でベクトルの長さを計算します。このベクトルの長さが主応力になります。つまり、長さが負になることはないので、事前に法線応力をプラス側にシフトしておく必要があるというわけです。計算が終了したら、このバイアス応力は差し引いておく必要があります。Bisection法でも主応力を計算できます。この方法は、三重根も正確に計算してくれました。ここで紹介した主応力の計算プログラムはPSST.FORで見ることができます。また、POST3DTAUX.FORで計算された応力τ_ijをファイルから読み込み、上で紹介した全ての方法で主応力とベクトルを計算するプログラムPRINCIPALSTRESS.FORも作成しました。