ここでは、Lanczos法で生成されたばかりの{r}_jを {r}^oldとし、再直交化された{r}_jを{r}とします。すると、再直交化は以下のように行うことができます。注意：{u}_i+1={r}/|{r}|。|{r}|は、ベクトル{r}の長さです。

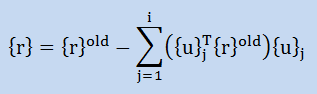
上式の正当性を確認するために、{u}₁が生成され、それをベースに{r}^oldが 計算された場合を考えてみましょう。すると、上の式は以下になります。

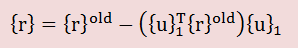
上式のスカラー量の{u}₁^T{r}^oldは理論的にゼロ ならなければならないのですが、数値計算上ではゼロになりません。 このゼロにならない値に{u}₁を掛け{r}^oldから引いたベクトルを {r}とすると、{r}^T{u}₁はゼロになるという仕組みです。 詳細については文献を調べてみて下さい。

この再直交化を行わないと計算結果に存在しえない固有値が現れてきます。 これは、おそらくLanczos法以外で三角対角化を行っても再直交化は必要になるのではと思っています。 実際にここにプログラムLANCZOS_PRINCIPLE_BASIC1.FORを添付しておきますので再直交化の部分を削除して計算を実行してみて下さい。固有値にどれぐらいの違いが出るか体験してみて下さい。
また、プログラムLANCZOS_PRINCIPLE1.FORでは、元の[A]と変換後の[T]の固有値と固有ベクトルをPower法、Jacob法、Bisection法([T]のみ)で計算するようになっています。固有値の違いをチェックしてみて下さい。
[T]の固有ベクトルは{u}₁の選択によって変化します。{u}₁を変えて計算してみて下さい。 ただし、{u}₁の長さは1になるようにして下さい。

これで[A]は精度良く三角対角行列に変換されたことになります。次は、上のプログラムでも使っている 三角対角行列の固有値を計算するBisection法を紹介します。Bisection法の長所と短所を 理解して頂ければ幸いです。