eigenvaluelanczos

Three Dimensional Finite Element Method
eigenvaluelanczos-15

最後に{v}^T{w}を計算してみましょう。結果はゼロになります。よって、以下のようになります。

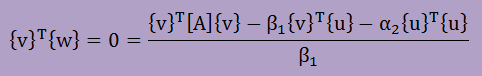
上式中の{v}^T{v}は1で{v}^Tu}はゼロですから、上式は以下になります。

以上のように、Lanczos法で[T]と{u}_iを生成すると、 [T]は三角対角行列になり{u}_iは{u}_jと直交(i≠j)していることがわかりました。この議論を拡張し、[T]がn×n行列に適用しても、三角対角以外の要素は全てゼロになることが解ります。

■[U]の再直交化処理■
これまでLanczos法による[U]の正規直交ベクトルの作り方と[A]の[T]への変換方法を説明してきました。しかし、実際にでLanczos法をプログラムすると[U]が正規直交ベクトルになっていないことに気付きます。これは有限桁の数値計算による様々な誤差が原因です。つまり、数値計算を行うと[U]を構成している {u}_iベクトルが互いに直交性が少しずつ崩れてゆく可能性があるということです。
そこで"再直交化"を文献調査するとGram-Schmidt法が検出されます。ここでは、この方法でプログラムしてみました。この方法の説明のために、以下の5つの{u}からなる[U]を考慮すると：

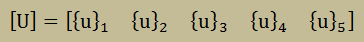
[U]を構成している{u}_iベクトルは、Gram-Schmidt法によって以下の直交性を満足させてくれます。以下はベクトルの内積(Dot product)を表しています。

が生成されたら	以下が満足されていること
{u}₂	{u}₁^T{u}₂=0
{u}₃	{u}₁^T{u}₃=0, {u}₂^T{u}₃=0
{u}₄	{u}₁^T{u}₄=0, {u}₂^T{u}₄=0, {u}₃^T{u}₄=0
{u}₅	{u}₁^T{u}₅=0, {u}₂^T{u}₅=0, {u}₃^T{u}₅=0, {u}₄^T{u}₅=0

計算結果がゼロと言うことは2つのベクトルが直交していることを意味しています。数値計算では、[U]を生成する過程で上記の直交性を徐々に失うという欠点があります。そこで考え出されたのがベクトルの再直交化です。それは、新しく{r}_iが生成されたときに{u}₁から{u}_iに対し{r}_iが直交するように再調整することです。

BACK	NEXT