同様に{δε}も次のように定義できます。
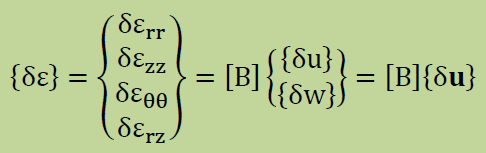
変位ベクトルの内訳としては、上で述べて通り半径方向(r)と長手軸方向(z)の2つがあります。すると上式中の変位ベクトル{u}は以下のように定義できます。プログラミングでは剛性マトリクスのバンド幅を小さくするために、変位uiと変位wiを交互に配置します。。
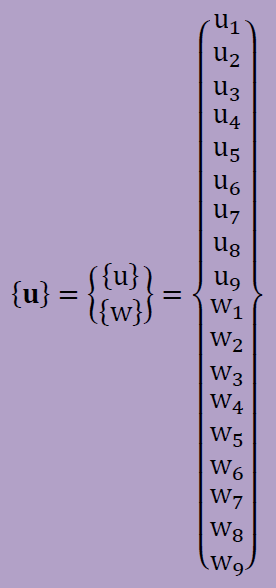
次は応力とひずみとの関係です。ひずみに材料定数群を掛ければ応力が得られます。材料定数群をマトリクスで表し、それを[D]と呼びます。等方性材料(isotropic material)の場合、下に示す[D] マトリクスは、ヤング係数とポアソン比のみで構成されます。軸対称の円筒座標系の[D]はGeneralized Hookeの法則より以下のように書けます。
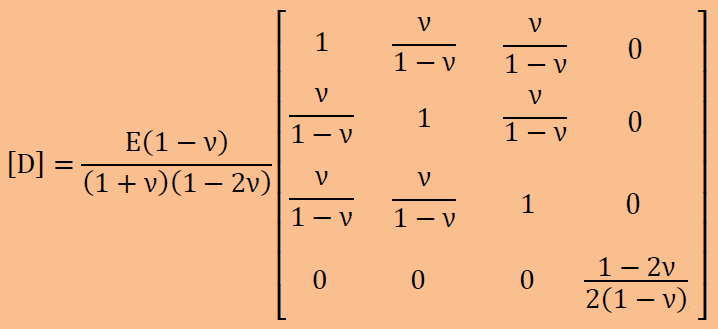
結果的に応力{τ}とひずみ{ε}との関係および変位ベクトル{u}との関係は以下のよう書けます。
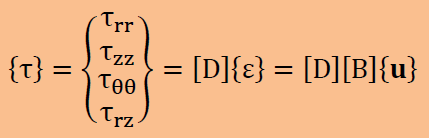
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |