そして、上で示した関係式の全てを積分式Iに代入すると、以下の結果が得られます。これまでに導いてきたマトリクス型の積分式とまったく同じスタイルをしていますよね。
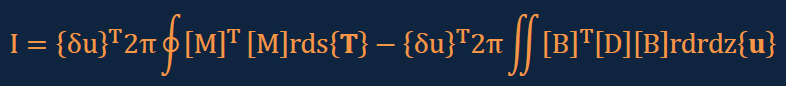
ここに、上の境界積分項にある{T}は以下のように書け、境界での外力を意味します。外力としては、圧力や摩擦力が考えられます。
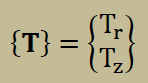
そして最後に積分式Iに対し∂I/∂δu=0と∂I/∂δw=0を施します。結果は以下のようになります。
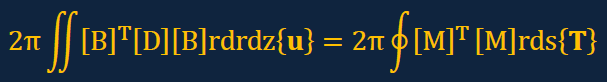
■プログラミングの前準備■
ここまでで理論とプログラミングに必要な材料は揃いました。ここからは、剛性マトリクスをプログラムするために作業を行わなければなりません。これが非常に大変な作業になり間違えることはできませんので、少しずつ話を進めて行きます。最初は[D][B]の展開を行ってみましょう。以下のようになります。
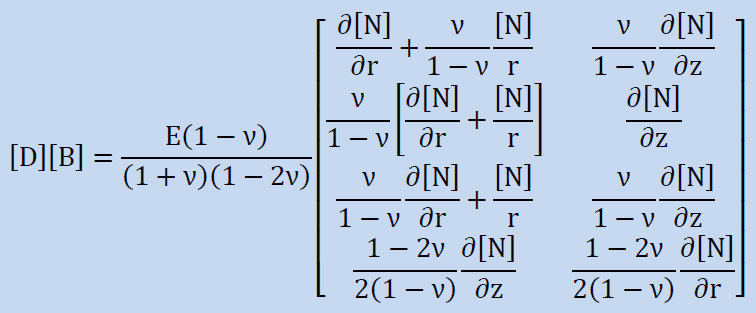
次に[B]T[D][B]の展開です。かなり複雑になります。通常のxyz座標系ですと[B]にリズムがあるため展開は容易でしたが。今回は、[B]に[N]/rが有るのでちょっとやっかいです。
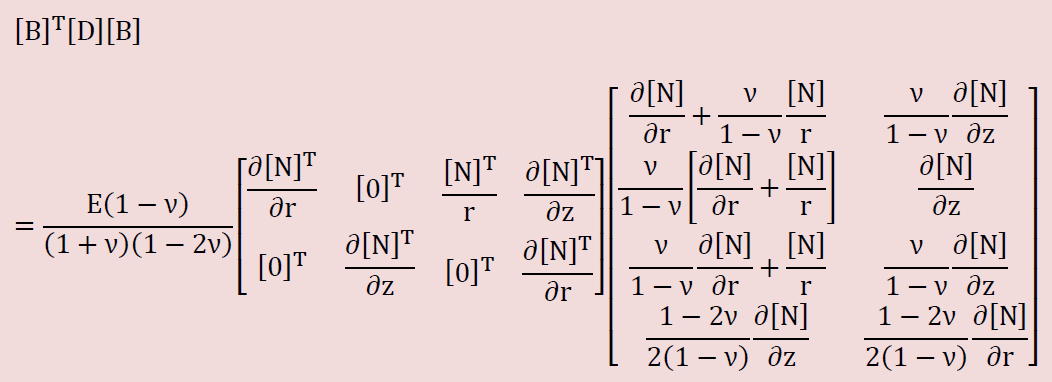
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |