| 変数名 | タイプ | 配列 | 役割/目的 |
|---|---|---|---|
| IBFORCE | 整数 | (MXBA) | Neumann型境界条件が与えられる節点 |
| BVFORCE | 実数 | (MXBA) | Neumann型境界条件が与えられる節点での境界値 |
| RHS | 実数 | (MXNA) | 連立方程式[K]{u}={RHS}の右辺 |
| AM | 実数 | (MXNA,MXWA) | 剛性マトリクス[K] |
| YOUNG | 実数 | 無し | ヤング係数 |
| POISSON | 実数 | 無し | ポアソン比 |
| NBW | 整数 | 無し | 未知数が1つの場合の連立方程式のバンド幅 |
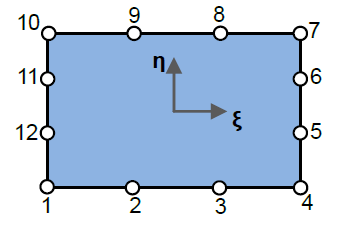
このプログラムの特徴として、2次元のparamで紹介した4-noded, 8-noded, 9-noded要素以外に下に示す12-noded要素が使えるということです。印の○が節点でその近くにある数字が要素の節点番号です。
筒形座標の特徴としては、支配方程式中に1/rが出てくることです。このプログラムでも剛性マトリクスの生成で1/rの計算が有りますが、Gauss-Legendre 積分法は節点を参照しないため、節点がr=0であっても問題なく積分できます。変位が得られた後、節点での歪と応力を計算する場合、節点がr=0になっていると、ゼロでの割算を行ってしまいます。ここで開発したソフトは、節点に限りなく近い要素内で変位、歪、応力を計算しています。
■計算例1:Pipe■
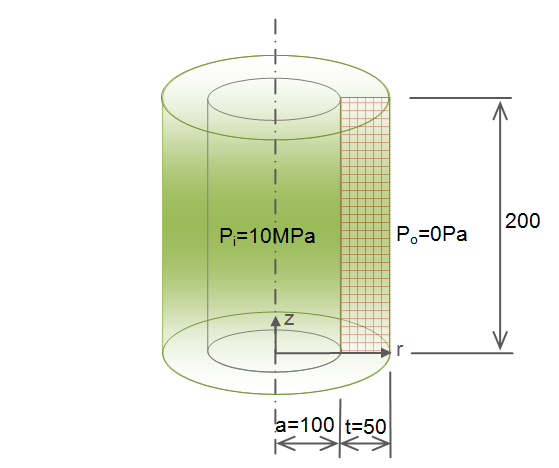
最初の例題は、極座標の部分に焦点を当てた解析を行ってみます。下図を見て下さい。肉厚が50mm、内径が100mm、長さが200mmのパイプの内側にNeumann型境界条件として10MPa、外側に0Paの圧力が掛かった状態を考えます。Dirichlet型の境界条件としては、底辺と状面のz方向を拘束してあります。半径(r)方向はfreeにしてあります。
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |