この条件下で肉厚にどのような応力が発生するか計算してみます。結果は厳密解のτrrとτθθと比較してみましょう。ヤング係数に210×109Pa、ポアソン比に0.3を使いました。計算は全ての要素で試してみました。計算領域を要素に分割するのは、上図の赤色でハッチしてある断面のみです。下に、要素分割の状況を示します。下表のプログラム名をクリックすると、データを作成するプログラムが表示されます。
| 要素 | r方向の 要素数 |
z方向の 要素数 |
データ作成 プログラム |
作成ファイル |
|---|---|---|---|---|
| 4-Noded Bilinear | 11 | 22 | SS4AXISYMM-TEST.FOR | STATIC4.DAT PARAM.DAT ELEMENT4.DAT |
| 8-Noded Parabolic | 5 | 10 | SS8AXISYMM-TEST.FOR | STATIC8.DAT PARAM.DAT ELEMENT8.DAT |
| 9-Noded Parabolic | 4 | 8 | SS9AXISYMM-TEST.FOR | STATIC9.DAT PARAM.DAT ELEMENT9.DAT |
| 12-Noded Qubic | 2 | 4 | SSCAXISYMM-TEST.FOR | STATICC.DAT PARAM.DAT ELEMENTC.DAT |
参考までに、12-Noded Qubic要素の分割状況を下に示します。
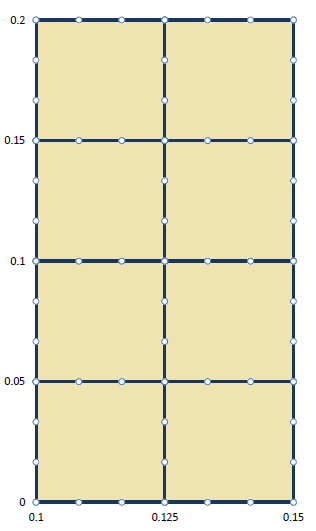
厳密解ですが文献を調べるとP0=0の場合以下の結果が得られています。この結果は応力関数がベースになっています。式の導出についてはTIMOSHENKO, THEORY OF ELASTICITY, 1970, McGraw-Hill, Inc.の68ページにあるStress Distribution Symmetrical about an Axisを参考にして下さい。
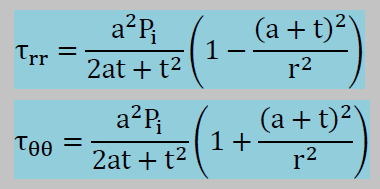
以下は計算結果です。図内の青い線は厳密解を示します。計算結果をみると、4-noded要素以外は、厳密解と高い精度で一致しています。
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |