ところが、要素分割を疎にするとτ_zzの精度は両境界面で異常な数値を示します。それに反し、τ_rrは常に安定した解が得られています。下図は、半径r方向を５要素、高さｚ方向を４要素で分割したときの厳密解との比較です。

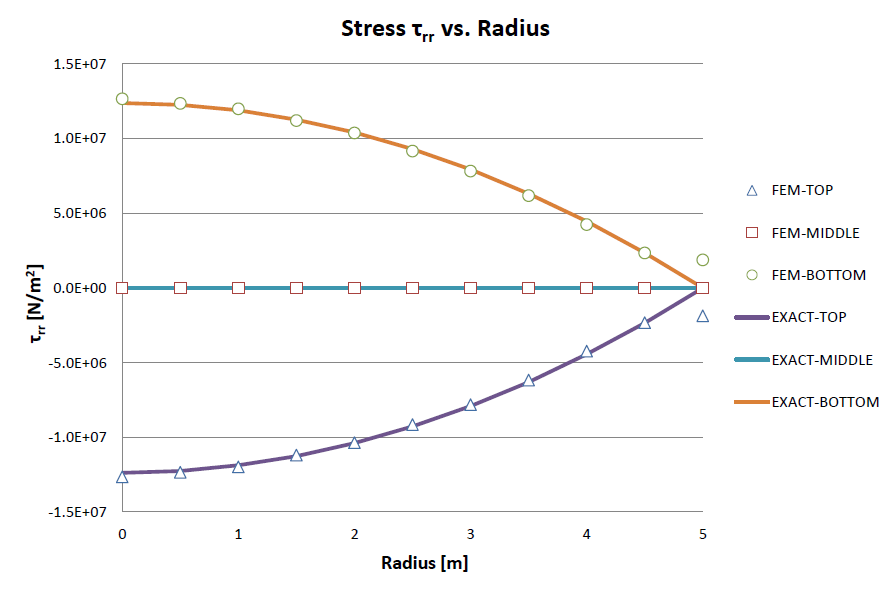
要素分割数は少なくてもτ_rrであれば厳密解と良く一致しています。図の凡例で示しているTOPは荷重面、MIDDLEは円盤の肉厚中心、BOTTOMは円盤の底面を意味します。
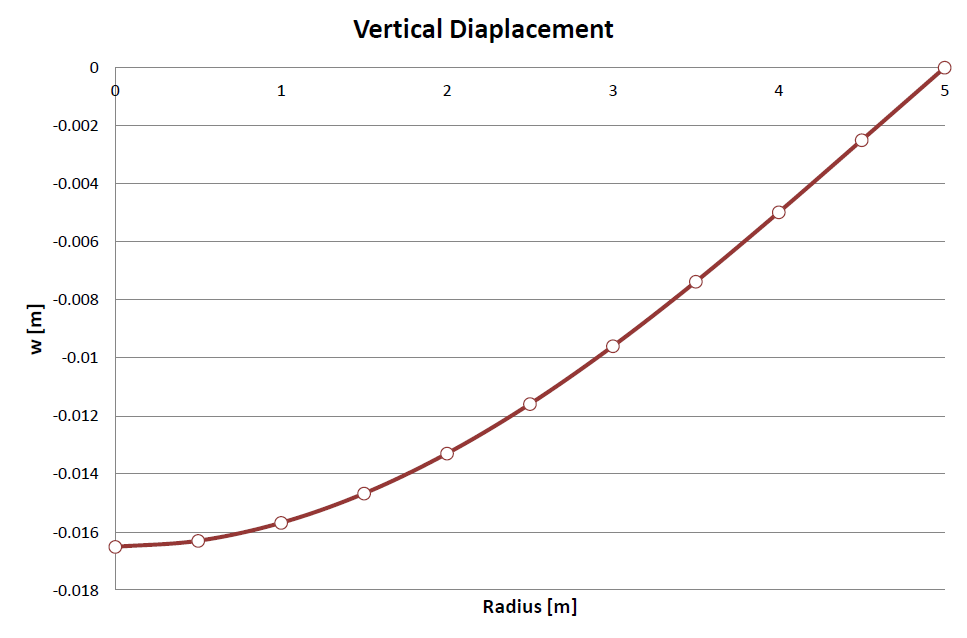
応力以外の計算結果もプロットしてみました。下図はz軸方向の変位wです。厳密解が無いので精度のチェックはできていませんが、見た感じ良い結果のようです。

以上で計算例は終わりです。今後時間をみて回転円盤(Timoshenco p388)の計算をやってみたいと考えています。この場合、生成項をカップルする必要があります。

次のページでは、ここのセクッションで使ったプログラムをリストしてあります。