上でも言っていますが、ω2=c2α2ですので、RadianとHzの定義から2πf=ωになり、つまり、 2πf=√(c2α2)ということになりましす。ここに、fは固有振動周波数f[Hz]です。 上の式を解くプログラムからは計算され変数λに入る固有値はα2ですから、固有振動周波数fは f=(1/2π)*c*√(λ)で計算されることになります。
しかし、固有値を解くためには、問題の定義式を[K]{x}=λ{x}の型に変換する必要があります。 また、上式の形では、最大固有値から最小固有値の順に求まるようになっています。 技術的には、最小か所望の固有値が要求されます。そのためには前に説明した シフトパラメーター(δ) を固有値に導入する必要があります。つまり、以下のように定義します。
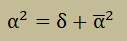
上式を固有値問題の定義式[K]{x}=α2[M]{x}の[K]に代入すると、以下が得られます。

ここに、シフトパラメーター(δ)を導入した後の”剛性マトリクス”は以下のようになります。

次に行わなければならないのが上の新しい定義式を[A]{x}=λ{x}の形に変換することです。
![]() {x}=α2[M]{x}に前から[M]-1をかければ出来ますが、この方法
だと
{x}=α2[M]{x}に前から[M]-1をかければ出来ますが、この方法
だと![]() [M]-1がフルマトリクス
になってしまいます。更に、シフトパラメーター(δ)が使えません。
そこで、[K]と[M]を三角行列に分解する方法で話を進めることにします。
[M]-1がフルマトリクス
になってしまいます。更に、シフトパラメーター(δ)が使えません。
そこで、[K]と[M]を三角行列に分解する方法で話を進めることにします。
まず、対称で正定値の形状マトリクス[M]は、以下に示すように三角行列に分解します。
| [M]=[B][B]T |
ここに、[B]は下三角行列を意味します。[B]の要素は、以下の式で計算できます。
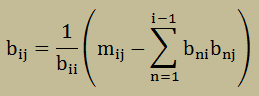
ただし、biiは以下の式で計算することになります。
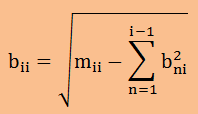
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |