Sound Eigenvalue

Three Dimensional Finite Element Method
Sound Eigenvalue-21

■計算精度■
例題を使って固有値の精度と要素分割数の関係を調べてみました。下図の縦軸は、厳密解-計算結果の差の対数表示です。横軸はX軸方向の要素数です。 Mode(1,0,0), (2,0,0)と(0,1,0)の固有値が表示してあります。

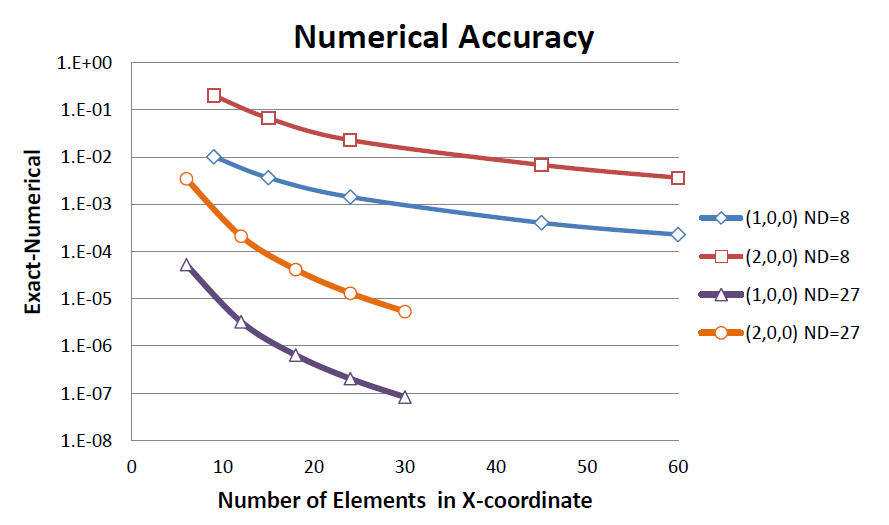
図の凡例でND=8が8節点ヘキサ1次要素です。1次要素ですから要素数を増やしても急激な精度の改善はありません。プログラム(前のページの表に示した全ての)を少々改良し27節点ヘキサ2次要素も使えるようにしました。凡例のND=27が2次要素を示す線です。入力データはMAKING-TEST-DATA27.FORで作成しました。プログラム中の NELEMENTを2, 4, 6, 8, 10と変えながら計算してみました。X軸方向の要素数はNEXです。 1次要素に比べ数段高い精度になっているのが解ります。
1次要素でもわりと少ない要素数で良い結果が出ています。分析したい周波数が事前にわかっていれば、その周波数の波長に 4要素が入るように要素の大きさと要素分割をすることをおすすめします。

==== 以下はここで紹介したその他のプログラムです。参考にして下さい。====

プログラム名	機能および目的
LANCZOS-SOUND10-JACOB-VT.FOR	3次元Helmholtz Eq.を固有値解析に従い離散化し、Jacobi法で固有値と固有ベクトルを計算する。
LANCZOS-SOUND11_0-BISECTION-VT.FOR	3次元Helmholtz Eq.を固有値解析に従い離散化し、Bisection法で固有値、Inverse Power法で固有ベクトルを計算する。
LANCZOS-SOUND11-BISECTION-VT.FOR	同上。しかし、Inverse Power法での固有ベクトル計算を行う際、[T]をバンドマトリスク化した。
LANCZOS-SOUND12-BISECTION-NEWTON-VT.FOR	3次元Helmholtz Eq.を固有値解析に従い離散化し、Newton-Raphson法で加速計算されたBisection法で固有値、Inverse Power法で固有ベクトルを計算する。
MAKING-TEST-DATA.FOR	8節点ヘキサ要素で離散化し、入力ファイルを作成する。
MAKING-TEST-DATA27.FOR	27節点ヘキサ要素で離散化し、入力ファイルを作成する。
ELEMENTCHECK.FOR	入力ファイルの要素形状をチェックする。
OPTIMIZER4.FOR	節点番号を付け替え剛性マトリクスのバンド幅を狭くする。

音響固有値の解析はまだ続きます。次は音響固有値を軸対称の円筒座標系で解いてみます。プログラミングとしては2次元ですが、3次元の形状を取り扱うことができます。

BACK	NEXT