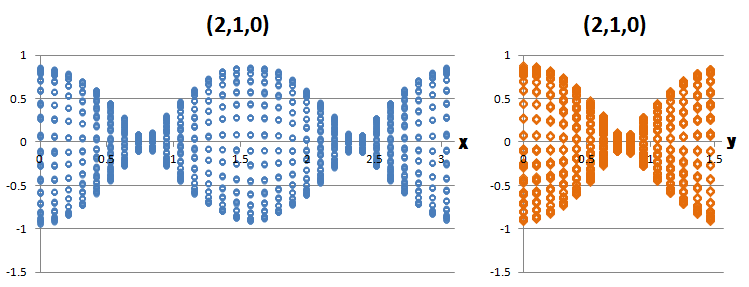
下はMode(2,1,0)です。この場合、2つの図で固有ベクトルを示してみました。左側は横軸がxで、右側の図はyです。 いつか2次元流体で紹介した平面プロットを試みるつもりです。すると、xy面に振動があることがわかります。
以上で例題はお終いです。
■プログラムLANCZOS-SOUND■
ここでは、LANCZOS-SOUND10-JACOB-VT.FORを紹介しましたが、その他幾つか類似のプログラムを
作ってみました。下の表にまとめておきました。
| プログラム名 | [T]用の 記憶サイズ |
固有値 計算方法 |
固有ベクトル 計算方法 |
|---|---|---|---|
| LANCZOS-SOUND10-JACOB-VT.FOR | m×m | Jacobs | Jacobs |
| LANCZOS-SOUND11_0-BISECTION-VT.FOR | m×m | Bisection | Inverse Power |
| LANCZOS-SOUND11-BISECTION-VT.FOR | m×2 | Bisection | Inverse Power |
| LANCZOS-SOUND12-BISECTION-NEWTON-VT.FOR | m×2 | Bisection/ Newton-Raphson |
Inverse Power |
射影された部分空間での固有値の計算に、ここではJacobs法とBisection法を使いました。両方法とも
問題無く重根の固有値も計算してくれました。
固有ベクトルの計算では、Jacobs法とInverse Power法
を使いました。これについては差が発生すると思っていました。と言うのも、文献を調べるとJacobs法は、
重根の場合でも正しい固有ベクトルを算出してくれるのに対し、他の方法はうまく行かないと言った記述を
大昔に見たことがありました。そこで、Inverse Power法によるMode(2,0,0)とMode(0,1,0)のベクトルを見ると、
問題なく正しい結果を出していました。ですからInverse Power法も問題なく使える方法だと思います。
最後に[M]の三角分解について触れておきます。今回は、[M]をassembleするときにlumpingを用いました。通常、時間項
には[M]に対しlumpingを行うと計算がとても安定します。そこで今回の場合も[M]にlumpingを施しました。多分、計算結果の
信頼性も高いと思います。
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |