次に、積分とSummationの結果を{F}とします。つまり、下に示す式がそうです。

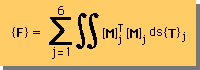
そして、{F}は、下に示す様なベクトルになっているはずである。

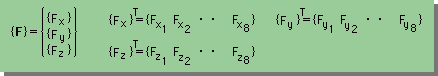
すると境界積分は、下式の様に表すことが出来ます。

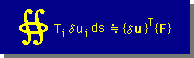
この式での{δu}^Tは、{δu}^T_j={{δu}^T {δv}^T {δw}^T}^Tであって、参考までに、
{δu}^T={δu₁ δu₂ δu₃ δu₄ δu₅ δu₆ δu₇ δu₈}であることに注意してください。

このままでは理解しずらいので、実際の例題で説明します。この例題では要素ごとではなく、Globalな{F}を計算する方法を紹介します。更に、3次元でなく、2次元の要素を使います。