ここでは、3次元弾性解析の積分式および有限要素式の導き方について説明します。これまでに取り扱ってきた微分方程式は、独立変数が1つでした。例えば、温度(T(x,y))。弾性解析での独立変数は、変位ベクトルですから、3次元の場合、u(x,y,z), v((x,y,z),w(x,y,z)の3つ要素になります。したがって、有限要素式から導き出されるMatrix式は、独立変数が1つのn*nに比べ、一挙に3n*3nの9倍に膨れ上がります。nは、要素上の節点数です。よって、[B]や[N]の計算は多少複雑になります。しかし、有限要素式を導く基本的な手続きは、以前に学んだ事柄と同じです。
■WRM■
WRMで有限要素式(積分式)を導くためには、Navierの式のResidualが必要になります。以下に、Residualを示します。
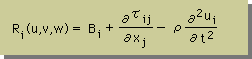
すると、積分式は次の様になります。

重み関数(δui)もベクトルになっていることに注意して下さい。
積分式ができあがると、次のステップはStressの項に部分積分を施します。結果的に、次の様になります。(参考:Navierの式を変位で表すと、Stressの項は変位の2階微分になる。)
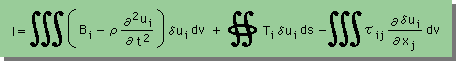
ここまで来れば、後は上式の各積分を要素の近似式で離散化するだけです。すると、要素の節点における変位(u,v,w)と要素に作用する外力を未知数とする、要素単位の積分式が生まれます。それでは、早速、項目毎に離散化を実施して行きましょう。
| BACK Navier | NEXT |
|---|
| Menu | Basics | Material | τ-ε | Failure | Navier | 3dim | 2dim | Sample |