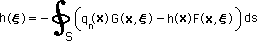Treatment of Free term Integrals
Taking Limits of Interior Equation
■疑問を感じる説明その2: Bounadry Equation■
境界要素法での2番目の疑問について説明します。今度もかなり深刻です。
前にも言いましたが、Interior Equation から Limit を使い Bounary equation を導くことは、まったくの間違った考えです。と言うより、Limit を使い Interior Equation のSource point ξ を境界へ 移動すること (または領域を小さくして) は不可能なのです。
Limitを使ってx→ξで関数 f(x-ξ) の状態を調べるということは、x=ξにすることではありません。xがξ近傍になったら関数 f(x-ξ) がどうなるかを調べることです。そのとき、x≠ξなのです。ですから、Limit の操作をおこなってもInterior point のxがBoundary pointになることはありません。
ですから境界積分式のSource pointがInteriorに有ればInterior equationに、境界に有ればBoundary equationになるのです。
まず、下に文献で紹介されている Interior Equation を表示しましょう。ここで、注意しておきますが、下の式は、ξ の点が境界線に触れない限り、領域内であれば、どこでも使える式です。また、h(ξ)は、領域内から境界にかけてスムーズな関数です。
文献では、上の積分の極限( interior ξ goes to bounadry ξ.)をとると、Boundary equation として、下の式が得られると言っています。境界線が、smoothな場合に限りますが。
この極限には、大きな無理が有ります。何故かと言うと、境界に限りなく近い領域内の点での h(ξ) は、境界の h(ξ) とほぼ同じ値であるはずです。しかし、上式の積分結果は、(1/2)h(ξ) になっています。つまり、境界の点で h(ξ) がジャンプ(急激に変化)したことになります。このことは、極限が存在しないことを意味しています。
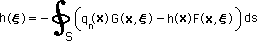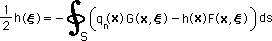なぜ、極限は存在しないかという疑問が残ります。答えは、下図に示す様に、C(ξ) が不連続な関数だからです。領域内から境界と境界から領域外へξが移動するときに、C(ξ) は、ジャンプします。このことから、C(ξ) のことを、Jump term とも言うことがあります。
