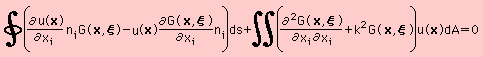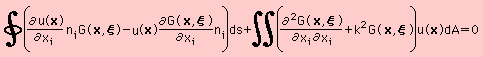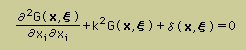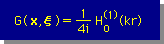Unbounded Region
2 Dim. Helmholtz Equation 03
部分積分をもう1回、領域積分のKernel function の微分の項に施します。すると、次の様になります。
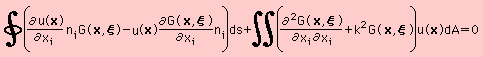上式の領域積分項に注目して下さい。
この積分項が定数で置き換えられると、境界積分のみが残ることになります。
つまり、下式を満足するG(x,ξ) が有るか無いかです。
もっと分かり易く言うと、”Helmholtz equation の Kernel function が存在するか”です。
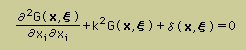ここに、δ(x,ξ) は、Dirac delta function です。
そして Laplace equation のところでも言いましたが δ(x,ξ) は次の様な特徴を持っています。
C(ξ) について前にも述べましたが もう一度 復習しておきます。
| ξの位置 | C(ξ) |
|---|
| 領域の中ならどこでも | 1. |
| smooth な境界(内角が180度) | 0.5 |
| 境界の点の内角がθ度 | θ/360 |
■Kernel function■
Helmholtz equation の Kernel function は、次の式で与えられています。
下式が本当に上の上の式を満足しているかいなかは、貴方にまかせることにします。
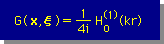ここに、r=|x-ξ| です。
H0(1)(kr) をHankel function of the second kind of order zero と言います。
BACK
NEXT
Menu
Laplace equation
Helmholtz equation