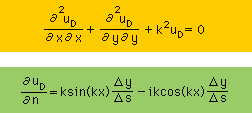
■Helmholtz equation を解く■
もう少しですので頑張って勉強を続けて下さいね。
次のステップは u = uI + uD を Helmholtz equation に代入して解くのみです。
uIは Helmholtz equation とSommerfeld radiation condition を満足していますから結果的に下のHelmholtz equation を構造物の表面での境界条件で解くことになります。
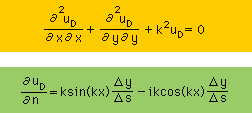
| K' = sqrt(uu*) |
| K' の値についてですが、仮に波を反射させる構造物がなかったら K' はゼロから1の範囲にあることになります。 理由は、cos2(kx)+sin2(kx)=1 ですからね。 また構造物にアプローチしてくる波と構造物から反射してくる波が重なり合う場合 K' はゼロから2の範囲になるはずです。 しかし 構造物にアプローチしてくる波は もっと沢山の反射波と重なり合うので 構造物(円柱と仮定した場合)の直径が波長より長い場合 K' の最大値は、2以上になると思われます。 |
| 無限領域の解析を行うときに注意しなくてはならないのが 積分の方向です。 無限領域内に置いた構造物は、hole(孔) ですから 積分の方向は時計方向になります。 |
■Program HLM8LINQ.FOR■
HLM8LINQ.FORは、Helmholtz equation を線形要素(linear element) で解きます。
プログラムの構造は、BEM8LINQ.FOR と殆ど同じです。
ただ違う点は 主要な変数が複素数(complex number)になったことと Kernel function を計算するサブプログラムが追加されたことと そして C(ξ) を計算するサブプログラムを BEM8LINQ.FOR から借用していることです。