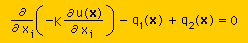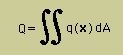■2次元問題の解決方法■
Point charge を吸収できない2次元では、どの様に計算すれば良いのかです。つまり、2次元の平面において、point charge を1つ置くことは出来ないということですから、考えられる方法は、符号の違う同量のpoint charge を2つ (+Q, -Q) 置けば良いことになります。下図の様になります。この様に、+Q,と-Q の構成をdoubletと言います。

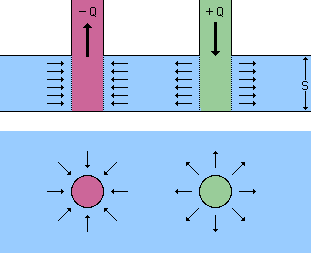上のdoublet の場合、正確には point charge でなく、分布(q)をもっています。すると、上図の状況でのポテンシャル(u)は、次の微分方程式で書けることになります。

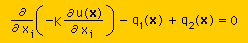ここで、q₁=q₂ です。そして、上式のqと上図のQの関係は、下式で表わすことができます。

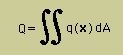結果的に、無限遠点で u(r=∞)=0 となります。また、このことは、無限遠点でsource 又はsink が無いことを意味していますので、∂u/∂n=0 ということにもなります。