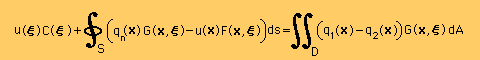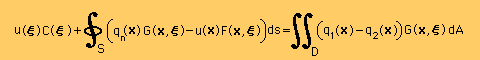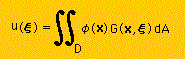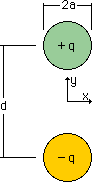Unbounded Region
2 Dimensional Laplace & Poisson's Equations 03
■積分式■
前のページの微分方程式にLaplace equation の kernel function をかけて積分し境界積分式を導くと次の様になります。
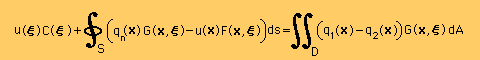 積分の領域(SとD)は無限大に長い閉境界線と無限大に広い面積であるということに注意して下さいね。
つまり境界(S)は無限遠の境界のみなので(孔は無いので)ξ点は全て領域内にあることになります。
よってC(ξ)=1 です。
そして、無限遠点ではu(r=∞)=0 と ∂u/∂n=0 ですから境界積分は上の式から消えてしまいます。
すると下式が残ります。
積分の領域(SとD)は無限大に長い閉境界線と無限大に広い面積であるということに注意して下さいね。
つまり境界(S)は無限遠の境界のみなので(孔は無いので)ξ点は全て領域内にあることになります。
よってC(ξ)=1 です。
そして、無限遠点ではu(r=∞)=0 と ∂u/∂n=0 ですから境界積分は上の式から消えてしまいます。
すると下式が残ります。
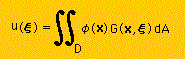 式を簡単にするために φ(x) = q1(x)-q2(x) としました。
上の式もφ(x)が存在(有限な値を持つ)している部分(Doublet)のみが数値を持ち それ以外の領域ではゼロを生産することになります。
式を簡単にするために φ(x) = q1(x)-q2(x) としました。
上の式もφ(x)が存在(有限な値を持つ)している部分(Doublet)のみが数値を持ち それ以外の領域ではゼロを生産することになります。
境界積分を勉強しているのに領域積分のみが残ってしまいましたね。
■例題■
計算式が出来上がったところで、早速、例題をやってみましょう。
まず下図を見て下さい。上下に2つの円があります。
上の円内に+q が等分布にそして下の円内に -q が等分布にあるとします。
円の半径 は、a で表わすことにします。
そして、2つの円の中心間の距離は、d で示します。
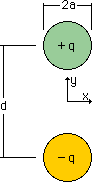
BACK
NEXT
Menu
Laplace equation
Helmholtz equation