さて計算ですが、要素は8節点1次ヘキサで分割し、z方向に10、y方向に15(z方向の1.5倍)、そしてx方向に30(z方向の3倍)の要素で分割してみました。 入力データはMAKING-TEST-DATA.FORで作成しました。データが 作成されたら、データのチェックをELEMENTCHECK.FORで行い、 OPTIMIZER4.FORでバンド幅の縮小を行います。 最後にLANCZOS-SOUND10-JACOB-VT.FORを実行します。参考までに、プログラムを実行するときに便利なのが.BATファイルです。私は例えばSUBMITA.BATを準備しておきます。 計算が終了後、ファイルEIGENVA-JCB08.LAZ(ここクリック)の固有値の部分を見ると以下のようになっています。左からMODE、固有値α2、流体が空気(c=340m/s)だった場合の固有振動数[Hz](注意:α2の単位を[m-2]と仮定した場合)、ERROR-IN-NORM=|[K]{x}-α2[M]{x}|/|[K]{x}|、そして一番右の列が固有ベクトルの信頼性判定です。固有ベクトルの信頼性判定で*印があるのは、ERROR-IN-NORM<eps(=0.001)になっているケースです。
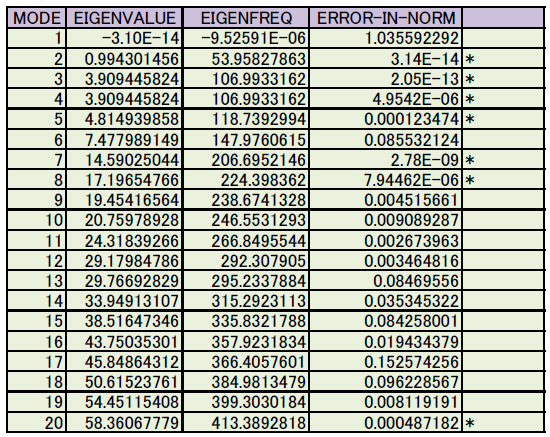
MODEが1の計算結果ですが、固有値がシフトパラメーターより小さいので信頼できる固有値ではありません。MODE=2はmode(1,0,0)を指しています。 固有ベクトルをプロットすると、以下のことが判明しました。
| MODE | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| Mode (i,j,k) | (1,0,0) | (2,0,0) | (0,1,0) | (1,1,0) | (2,1,0) | (3,0,0) |
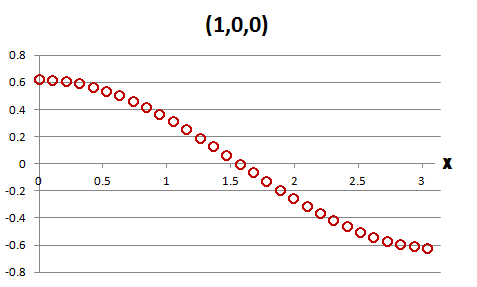
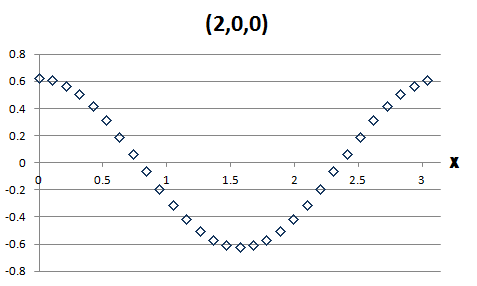
下の図はMode(1,0,0)と(2,0,0)です。この図は、全ての節点の固有ベクトルの値を縦軸にそして横軸は節点の座標値 です。Mode(1,0,0)と (2,0,0)の横軸はxです。ですから、図の1点は11×16(y方向の節点数×z方向の節点数)=176の値からなっています。全てが1点に集約されているということは、純なMode(1,0,0)と (2,0,0)ということです。
| BACK | NEXT |
|---|
| Menu | LU Decompo | Stiff | 3D Solid | 3D Fluid | Eigen&Lanczos | Sound Eigen | Solid Eigen | Solid Axisym |