■運動方程式■
応力の式が定義できれば、運動方程式(運動量の保存の式)の境界積分のTiをτijnjで置き換えることができます。その前に、境界積分に対してDivergenceの定理を施すと、運動方程式は、次の様に書き表すことができます。
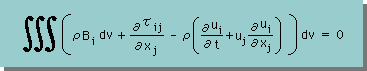
そして、Poisson のτijを代入し、積分領域の任意性を適合すると、運動方程式は、次の様になります。また、この運動方程式をNavier-Poisson equations といいます。
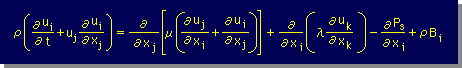
Dkk=divV=∂uk/∂xkです。 上式のindex i は、free index ですから、通常のx,y,z座標系で書くと、3つの式になります。
ここで、もう一度、言っておきますが、上の式は、質量の保存はbuilt-in されています。つまり、流体の流れが非圧縮性 ( divV=0 ) かどうかは、第2粘性係数(λ)の数値如何によることになります。
第2粘性係数(λ)の存在を理解してもらうために、次の様な究極の実験装置があったらいいな、と、いつも思っています。その実験装置には、2つのつまみがあり、1つを回すとμが変化し、もう1つを回すとλが変化します。そして、この実験装置を使い、様々な流れや様々な周波数の音の伝播のデモンストレーション行います。見学者は、立ち所に第2粘性係数の特性や役割を理解してもらえるのですが。
弾性力学でも、同じ様な究極の実験装置を考えられます。つまり、Young係数とPoisson比のつまみがある実験装置です。勿論、この実験装置をコンピューター上で実現することは、簡単ですが。
■Navier-Stokes の式■
話しを運動方程式に戻します。上の運動方程式とNavier-Stokes の式の違いを説明しておきます。Navier-Stokes の式には、λの項がなく、PsがP(平均圧)で置き換わっています。つまり、流体の力学特性をμのみで表していることになります。正確に言うと、μ/ρが一致すれば、いかなる流体でも、流れは同一であるとNavier-Stokes の式は、言っていることになります。
Navier-Stokes の式で、もう1つ気になる点が有ります。それは、連続の式が満足する速度ベクトルと、Navier-Stokes の式が満足する速度ベクトルに多少のずれがあるのではないかということです。Navier-Stokesベースの数値計算の結果を観察すると、速度ベクトルは、スムーズな解になっているが、圧力は、かなり不安定な値を示しています。ここで紹介しているNavier-Poisson equations では、λdivVの項が、このずれを吸収していると考えられます。
| BACK | NEXT |
|---|
| Menu | Govern | FEM | 2nd Visco | DCF | Cylinder | /Heat | Lub |