誤差が最大で0.003%になっています。このことからも、精度は分割数に左右されないことが分かります。ただし、12節点要素は、固有値の対応にやや問題がありそうです。

■NEX=100の場合の4-noded Iso-parametric要素の精度■
9節点と12節点要素では、分割数に関係なく計算精度は安定していました。問題は4節点要素です。要素の節点間の要素の変形が直線で近似されているので、曲げには対応しにくにと考えられます。 まず、4節点要素がどんな特徴を持っているのか簡単な計算をしてみましょう。横方向の分割数(NEX)は100に固定して話を進めます。積分ルールは一般的なGauss-Legendreの2点法を使います。下図は4節点要素で計算した場合の半径Rの計算誤差を示します。グラフの横軸が縦方向の分割数(NEY)です。計算誤差は、NEY=20でも0.4%がやっとです。9節点要素の2×4(NEY×NEX)要素分割による計算結果と比較しても10倍の誤差になっています。9節点要素の2×10要素分割に対しては約100倍の違いがあります。しかも縦方向の分割数(NEY)の変化に対し、誤差が大きく変動します。つまり、ロバスト性が低いことになります。このままでは使い物になりません。

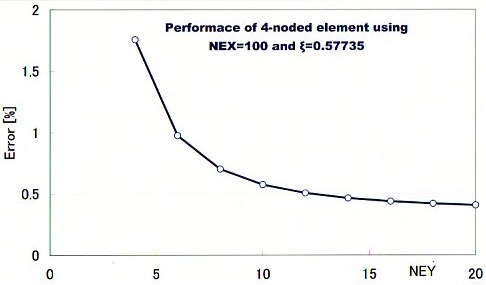
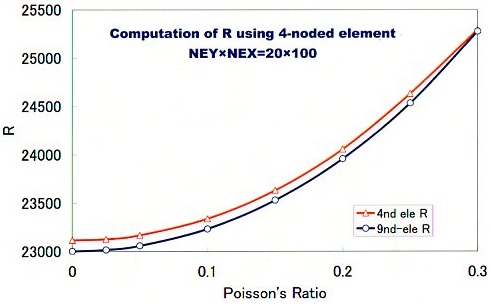
誤差の計算方法が(計算値-収束解)/収束解×100でしたから、上のグラフは半径Rが収束解より大きいということを示しています。つまり、曲げ難い要素であるということです。ついでにPoisson’s ratioとRの関係の計算もやってみました。下図には、4-nodedと9-nodedの計算結果が示されています。横軸はPoisson's ratioです。

ではどうすれば、より曲がるようになるのか。有限要素法の計算手法の何を改善すれば曲がるようになるのか。ここで大切なのが、有限要素法の基本ルールは変えないことです。何も足さない、何も引かないということです。計算結果の変化を与える方法として以下が考えられます。
(1)積分ルールを変える(Gauss-Legendre法だけが数値積分法ではない)。
(2)重み関数に非Galerkin法を使う(有限要素法の特徴)。

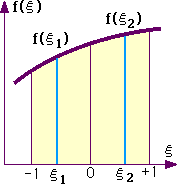
上の(2)ですが、本サイトで紹介しているプログラムの殆どがGalerkin法で重み関数を決めています。近似関数の一部を用いない重み関数の例としてfem\1dim\wrm\wrm7.htmalで紹介したWRM2X2H.FORがあります。このプログラムを実行すると、Galerkin法のWRM2X2.FORと違った結果が出力されます。しかし、どのような重み関数が適切かを選ぶのは大変な作業になります。そこで、文献等で取り上げられている(1)に関する低減精度積分法で計算結果に変化を与えることにします。下図は、2点法でf(ξ)を-1から+1までを積分する様子を示しています。