HAM-General

General Information

■きっかけ■
最近(2021年)オフセンター80-meterダイポールアンテナを家の周囲に張りました。 80m, 40m, 20mで快適に運用できました。給電点はアンテナ長の1/3の位置にあります。 80mでは、インピーダンスミスマッチでリグの内にあるチューナーを使っていますが、 40mと 20mでは基本チューナーは不要です。
その時にネットの情報を参考に1:4のバランを作製し偶然にも満足の行くものが出来ました。その後、アンテナとバランの性能を記録に残そうと思い、もう1つ1:4のバランを作りました。ところがいくら試行錯誤を繰り返しても満足の行く物はできませんでした。
そこでネットや書物(特にトロイダル・コア活用百科)を読んでやっと理屈が分かりました。 100%理解しているわけではありませんが、満足の行く1:4のバランが出来ました。まだ改良の余地が有ると思いますが。HF帯ではSWRが1.1以下で、30～110MHzまでは、SWR1.1から1.2でした。

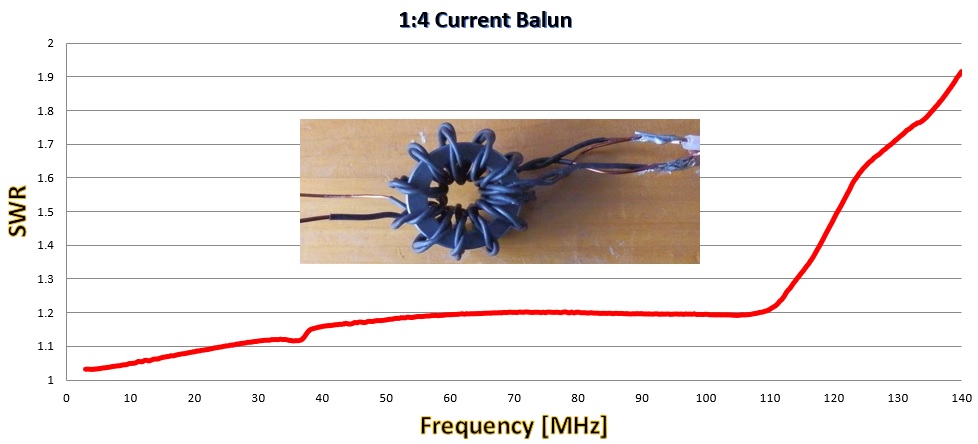110MHzは急にSWRが悪化しているのは、Ni-Znフェライトコアを使ったせいだと思います。 2線を撚線にしてあるのは、密着性をよくするためです。次回は撚線にしなくても密着性が向上する方法を試みてみます。
問題はコアに巻き付ける平行２線の伝送線路(transmission line)の特性インピーダンスでした。1:4(50Ω対200Ω)の場合コアに巻き付ける2線のインピーダンスは、50×200の平方根の100Ωでなければなりません。 100Ωにするには、線間の間隔が問題になって来ます。これを解決するには、並行２線の間隔を変えながら、電流及び電荷を与えたときの磁界からインダクタンス(L)と電荷からキャパシタンス(C)をそれぞれ割り出し特性インピーダンス(√(L/C))を計算する必要があります。
ネットで上記の問題解決に関する記述を探していましたが見つかりませんでした。唯一見つかったのが、海外の文献で以下のような内容でした：”コアに巻き付けているのはトランスではなく、平行２線の伝送線路です。２線は出来るだけ密着させなければなりません。そうでないと、特性インピーダンスが途中で変化してしまう。”
電磁気学の書物を見ると、LとCはポアソン微分方程式を解くと得られることが分かりました。そこで、ここでは私が理解した範囲で微分方程式を導き、境界要素法(BEM) と有限要素法(FEM) を用いLとCを求める手順をここにまとめてみました。内容に間違いや理解不足等がありましたら連絡下さい。
電磁気や波の解析では、無限領域を扱うことが多いです。その理由からここでは、境界要素法を多く使っています。しかし、キャパシタンスの計算の場合、複数の材料で誘電率が異なる場合は、有限要素法が便利です。

■数学的処理と数値計算処理■
ここでは、インダクタンス(L)とキャパシタンス(C)を計算する方法を紹介する前に、微分方程式を導くことから行います。そうすることにより解く微分方程式の特徴を理解でき、考慮しなければならない境界条件が明確になります。ここでは、Ampere's LawとGauss's Lawが出てきますが、これらは解く微分方程式の境界条件に深く関係しています。
境界要素法と有限要素法を勉強していると必ず問題を支配している法則に遭遇します。それらの法則を理解することが、境界要素法と有限要素法に理解を深めることに繋がります。

解析用のソフトを開発するときは、まず微分方程式を離散化が楽に行える段階まで、数学処理を行います。次は、数値計算法で離散化しフローチャート化します。数学処理が少ないと離散化で苦労することになります。その代表が差分法です。差分法では法則を理解することなく数値計算が行えます。ですので間違った境界条件を与えてしまうことが有ります。
しかし、数学処理が多いと離散化は楽になり解析精度は格段に向上しますが、数学的な拘束が大きくなり、応用範囲が少し狭くなります。その代表が境界要素法です。境界要素法による数値計算が成立するには、微分方程式を無限領域で満足するGreen関数が必要です。電磁気学では無限領域が必須ですのでメリットと言えます。
インダクタンス(L)とキャパシタンス(C)の計算では、ポアソン方程式を解きます。電流または電荷のソースとシンクが点だとラプラス方程式のGreen関数で計算を進められますが、電流または電荷が面で存在していると、領域積分が必要になります。ここでは、領域積分を行う境界要素法と境界にAmpere's LawとGauss's Lawによる境界値を与える境界要素法を紹介しています。

それから電磁気の書物やネットを見ると、以下の式が平行2線のLとCの近似式として出てきます。これがどの様にして導き出されたのか、どの様な条件でどんな微分方程式を解いて得られたのかが不明でした。ここでは下式がどの様にして得られたか明らかにしています。

\begin{eqnarray} f_3=\frac{1}{\pi}{log}_e\left(\frac{D+\sqrt{D^2-4a^2}}{2a}\right) \end{eqnarray}

つまり平行2線のLとCは、L=μf₃, C=ε/f₃で近似できます。