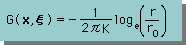
前ページの条件に満足するのが、下のKernel function です。 前にも言いましたが Laplace equation の場合のKernel をGreen function とも言います。 分母に係数Kがあることに注意して下さい。 Fundamentalsで紹介したKernel functionにはKがありませんでした。

■Boundary Element Equation■
話しをResidualの積分式に戻します。 有限要素法と同様に、まず2階微分項を部分積分を使って境界積分と領域積分に分解します。 すると、下のGreen's First Identity が生まれます。 今から考えると、有限要素法は、Green's First Identity がベースになっていたことになります。
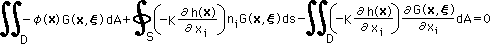
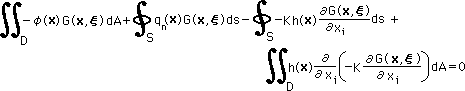