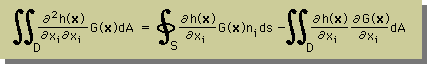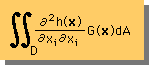
有限要素法や境界要素法に関係した数値解析を勉強していると、様々な法則や方程式に遭遇します。 その中で、一際目立つのがGreen's Identities です。 解析学で重要な式の1つですので、しっかりと勉強し理解して下さい。 また Green's Identities は 境界要素法と密接な関係にあります。
ここでは、まず、Green's Identities を導きます。そして、Laplace equation 用の境界要素法の基礎式を導きます。
■Green's Identities■
Green's Identitiesを説明するために、まず、関数 h(x,y) と G(x,y) を用意します。
式の中では、記述する文字数を減らすために、h(x,y) と G(x,y)の代わりにh(x) と G(x) の様に記述するときもあります。
次に、関数 h(x,y) を Laplace operator に代入し、関数G(x,y) を乗じます。
つまり、L(h(x,y))G(x,y) です。ここに、L(h(x,y))=h,ii です。
そして、この積を下に示す様に領域積分します。有限要素法と同じですね。
丁度、L(h(x,y))が、残差 R(u) で G(x,y) が重み関数といった感じになっていますね。
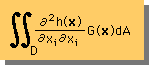
そして、上のLaplace に対して部分積分を施します。 すると、上の積分は 下式の様に境界積分と領域積分に分離することができます。 ここまでは 有限要素法とまったく同じです。