Two Dimensional Boundary Element Method
Discretization by Constant Element
これまでのところは、理解できましたでしょうか。
ちょっと難しかったり、ちょっと見慣れないシンボルだったりして、理解に苦労すると思いますが、頑張って下さい。
さて、ここでは、境界積分式の離散化を勉強します。
有限要素法で学んだ形状関数をベースに話しを進めます。
後程、紹介しますが境界要素法では有限要素法と違って、境界の離散化にconstant element (一定要素) が使えます。
境界要素法で最も簡単で基礎になっている要素ですので、しっかり勉強して理解につなげて下さい。
■Element■
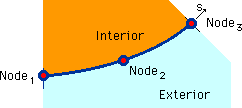
2次元の境界要素法では、領域の境界上を線積分するために、境界を適当な数の線要素で分割します。
下に2次の線要素を示します。丁度、1次元有限要素法の2次要素に似ています。
上の要素の形状関数にしたがって変数 h(x) 及び qn(x) を近似すると、下式の様に書き表わすことが出来ます。
この表現方法は、有限要素法の境界要素とまったく同じです。
要素の形状関数については、Parametric element のところで詳しく紹介します。
変数の近似式が出来たので、次は境界積分式の離散化です。
積分式のh(x) と qn(x) を近似式で置き換えます。
そして、閉線積分が、要素上を積分する線積分の和で表わされることになります。下がその結果です。
尚、微分方程式のφ(x) は、ゼロとしました。
つまり、解こうとしている微分方程式は、Laplace equationということになります。


BACK to Formulation
NEXT
Menu
Fundamentals
Formulation
discretizatione
Example
Straight
Multi-D