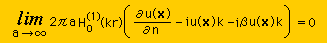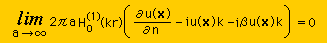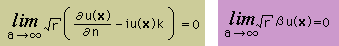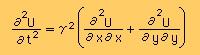Unbounded Region: Helmholtz Equation

Unbounded Region
2 Dim. Helmholtz Equation 11

距離 r が大きくなると Bessel 関数と Neumann 関数の関係は J₁=N₀とN₁=-J₀になります。これは、この図とこの式を見れば明らかです。つまり -iH₁⁽¹⁾=H₀⁽¹⁾ になります。すると ds=adθ から上式は次の様に書けます。

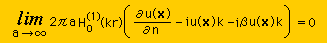ところで Hankel 関数(H₀⁽¹⁾)ですが r が大きくなるとこの式から H₀⁽¹⁾ は sqrt(1/r) に比例することが分かります。そして領域の半径である a は a が大きい場所では a=r として差し支えありません。よって上の極限の式は次の2つ分割できます。

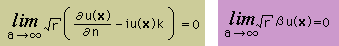上の2つの条件が満足されると、無限境界上の積分をゼロにすることができることになります。特に、kがゼロでない時、上式の2つの式をSommerfeld radiation condition と言います。式の意味は、無限点において、sources of radiation が無いことを意味しています。

上の右の式のβについてですが、領域が大きくなると a=r になります。よって β＝0 になります。つまり u(x) が無限点においてゼロになる必要はなさそうです。詳細な議論については、Sokolnikoffを見て下さい。

ここら辺で一服してください。

■水面波への応用■
水面上の波には、線形波と非線形波に分類できます。非線形波の1つにサージがあります。つまり津波です。ここで取り上げる波は津波の様に複雑な波でなく波長の長い線形波に限定します。すると水面波は下の Wave equation で追跡できます。

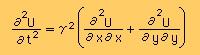ここに U(x,y,t) は波の高さ(tpography function)を意味します。 γは wave velocity です。