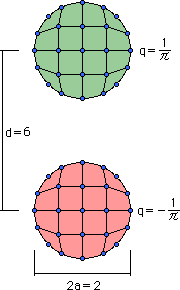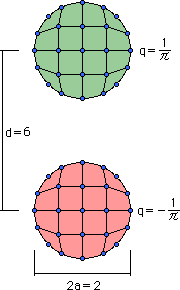Unbounded Region
2 Dimensional Laplace & Poisson's Equations 05
4-noded iso-parametric 要素で分割すると下図の様になります。1つの円を16の要素で分割しています。
図の中の青い点は、節点です。
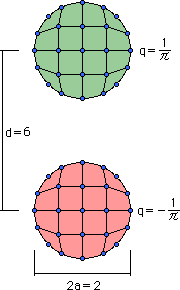図には節点番号が付けてありませんが皆様は入力データファイルのDOMAIN.DATを見ながら節点と座標値を確認して下さい。
またこのデータファイルは、SET3.FORで自動生成されます。
Internal points は y 座標軸上に、50点設けました。
■Program: DOMAIN.FOR■
このプログラムは前に紹介した積分式を与えられたinternal pointの座標値(ξ)にしたがってただu(ξ)を計算するだけです。
下表に計算を行うための主なSubroutine を紹介します。
| Subroutine 名 | 役 割 |
|---|
| SHAPEF | 形状関数を計算する。 |
|---|
| DERIV | 形状関数の微分を計算する。 |
|---|
| GDM | [N]T[N]を計算する。 |
|---|
| INDCTAJ | u(ξ)を計算する。 |
|---|
プログラムはいたって簡単です。
連立方程式を計算する必要もありません。
ただしInternal point の座標値(ξ)の決め方に注意して下さい。
Internal point の座標値が節点の座標値と同じになると r=0 になりDivided by zero のfloating point error になります。
また、節点に接近した位置もよくありません。
誤差が大きくなります。
それから SET3.FORでは d の値を画面から入力する様になっています。
画面では d/2 を入力するように聞いてきますので注意して下さい。
つまり d=6 の場合 3を入力します。
BACK
NEXT
Menu
Laplace equation
Helmholtz equation
