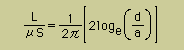Unbounded Region
2 Dimensional Laplace & Poisson's Equations 08
■導線の表面(Skin)に電流が流れる場合■
導線を流れる電流が電磁誘導による交流電流になると話しはちょっとややっこしくなります。
周波数が低い場合は直流電流と仮定して自己インダクタンスを計算できますが周波数が高くなると電流が導体の表面を流れる様になります。
特に導電率の高い導線でこの現象は顕著に現われてきます。
つまり電流が流れる方向に対し直角方向への電流の減衰が大きくなることを意味しています。
減衰の大きさと周波数×導電率は、比例します。
Maxwell equations から導き出される波動方程式(Helmholtz equation) を解くとこの比例関係がよく見えてきます。
そこで非常に高い周波数の交流電流が導線を流れることを考えてみましょう。
すると下図に示す様に、電流は、導線の表面を流れることになります。
実際は波動方程式であるHelmholtz equation で計算すべきでありますが ここでは簡易的に Laplace equation で磁気ベクトルポテンシャルを計算してみます。
つまり電流を境界条件として与えます。
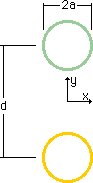 前回と同様に、Q=1 とします。
そして Qが半径(a)=1 の導線の表面を等分布に流れるものとします。
すると表面(s)の単位長さ当たりに流れる電流は q(s)=1/(2×π) になります。
この場合の自己インダクタンス値の厳密解は下式で得られます。
詳しいことは John D. Kraus の
Electromagnetics, 4nd Ed., MacGraw-Hill, 1991 を参考にして下さい。
前回と同様に、Q=1 とします。
そして Qが半径(a)=1 の導線の表面を等分布に流れるものとします。
すると表面(s)の単位長さ当たりに流れる電流は q(s)=1/(2×π) になります。
この場合の自己インダクタンス値の厳密解は下式で得られます。
詳しいことは John D. Kraus の
Electromagnetics, 4nd Ed., MacGraw-Hill, 1991 を参考にして下さい。
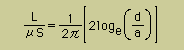
BACK
NEXT
Menu
Laplace equation
Helmholtz equation