Three Dimensional Finite Element Method
3D Solid Example-20
■シャフトのねじり剛性■
Shear Lockingの調査としてシャフトのねじり(Twist)を計算してみました。ねじりに関しては本サイトの
Torsion
を参考にして下さい。
まず、下図にここで取り上げているシャフトを示します。Young Modulus E=69.×106, Poisson's Ratio=0.3を使っています。これらの値は、
ビームの自由端にモーメントMが作用している場合
で使っています。
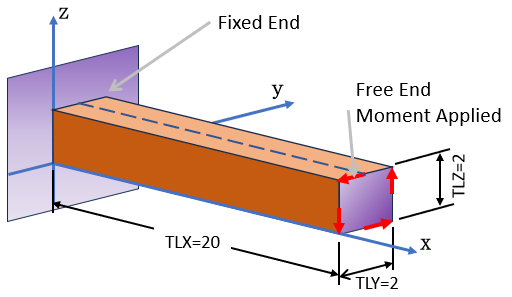 上図の自由端にはねじりを与えるために4つの力(1000[N])が掛かっています。Arm Lengthが1[m]ですので、モーメントは4000[Nm]
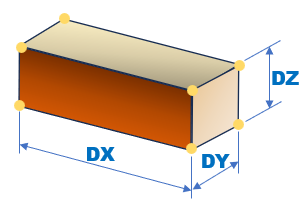
になります。シャフトはShear Lockingの調査を行いますので8節点1次ヘキサ要素を使います。以下に1つの要素を示します。
コーナーの●が節点です。
上図の自由端にはねじりを与えるために4つの力(1000[N])が掛かっています。Arm Lengthが1[m]ですので、モーメントは4000[Nm]
になります。シャフトはShear Lockingの調査を行いますので8節点1次ヘキサ要素を使います。以下に1つの要素を示します。
コーナーの●が節点です。
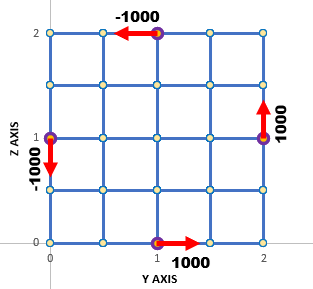
 下はシャフトの断面方向に4要素×4要素で分割した状態を示します。そして自由端に4つの力を与えた状況を示しています。縦軸がz座標、横軸がy座標です。TLY=TLZ=2[m]ですから、要素の長さDY=TLY/4=0.5[m]になります。高さもDZ=0.5[m]になります。
下はシャフトの断面方向に4要素×4要素で分割した状態を示します。そして自由端に4つの力を与えた状況を示しています。縦軸がz座標、横軸がy座標です。TLY=TLZ=2[m]ですから、要素の長さDY=TLY/4=0.5[m]になります。高さもDZ=0.5[m]になります。
 上図の要素分割を使って計算してみました。このときx軸方向を要素数10~24で分割しRate of Twist(θ)を計算します。この時DXは2から0.8333まで変化し、Aspect比としては4から1.66666まで変化します。下図はこの条件でのRate of Twist(θ)の結果です。
上図の要素分割を使って計算してみました。このときx軸方向を要素数10~24で分割しRate of Twist(θ)を計算します。この時DXは2から0.8333まで変化し、Aspect比としては4から1.66666まで変化します。下図はこの条件でのRate of Twist(θ)の結果です。
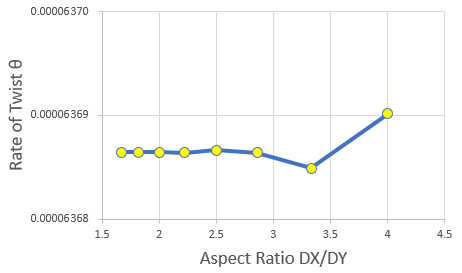 Aspect比が2.5(DX=1.25)で数値は落ち着いています。これ以上DXを小さくする必要はありません。
Aspect比が2.5(DX=1.25)で数値は落ち着いています。これ以上DXを小さくする必要はありません。
今度は、NEY(y軸方向の要素分割数)とNEZ(=NEY)を2から24まで変化させRate of Twist(θ)を計算してみました。下図がその時の結果です。図にConvergence value of θとありますが、これは27節点2次ヘキサ要素を使って得られた計算結果です。詳細は
Torsion3次元解析
を見て下さい。結果としてθ=0.0000670055862315403を得ています
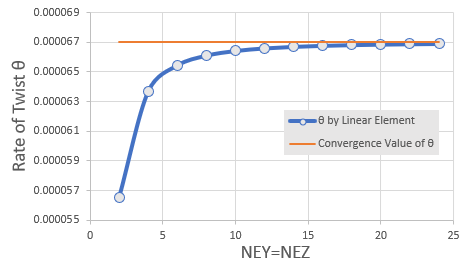 8節点1次ヘキサ要素でもNEYとNEZを大きくすると収束値に近づきつつありますが、Shear Lockingが影響し収束速度が遅いです。そこで、Free Selection法の低減精度積分を使いGauss-Legedreのsampling座標ξを求めてみました。計算ではNEX=20, NEY=NEZ=8を使いました。Gauss-Legedre 2点法のsampling座標は、ξ=±0.577350269189625です。下が結果です。横軸がGauss-Legedreのsampling座標ξです。
赤丸の点がGauss-Legedre 2点法のsampling座標を使っての結果です。
8節点1次ヘキサ要素でもNEYとNEZを大きくすると収束値に近づきつつありますが、Shear Lockingが影響し収束速度が遅いです。そこで、Free Selection法の低減精度積分を使いGauss-Legedreのsampling座標ξを求めてみました。計算ではNEX=20, NEY=NEZ=8を使いました。Gauss-Legedre 2点法のsampling座標は、ξ=±0.577350269189625です。下が結果です。横軸がGauss-Legedreのsampling座標ξです。
赤丸の点がGauss-Legedre 2点法のsampling座標を使っての結果です。
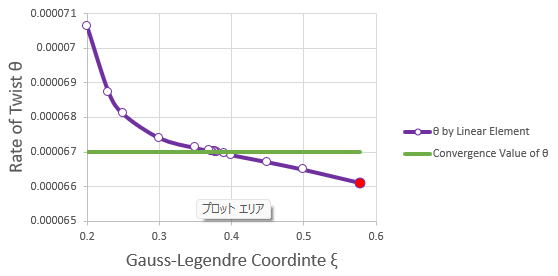
ξ=±0.3769で27節点2次ヘキサ要素を使っての結果と同じになています。今後NEYを変化させ計算を行ってみたいと考えています。
これで3次元線形弾性解析の計算例はこれでおしまいです。次は、3次元流体を紹介します。
BACK
3D Fluid
Menu
LU Decompo
Stiff
3D Solid
3D Fluid
Eigen&Lanczos
Sound Eigen
Solid Eigen
Solid Axisym
Internet College of Finite Element Method






