Torsion
3 Dimensional Torsion Analysis
■3次元弾性解析■
2次元のStress Functionによる計算結果の解析精度を検証するために、3次元の弾性解析を行いました。
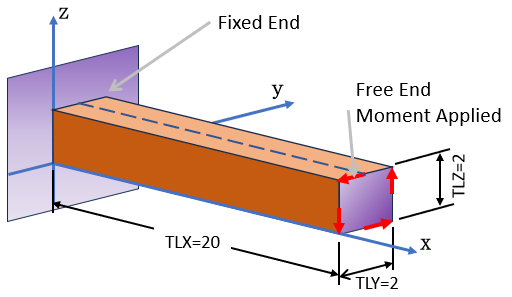
シャフトの拘束条件と自由端での力の設定を下図に示します。赤の矢印で示しているのが力の方向で値は1000[N]です。
図に示す破線上でy方向の変位v(x,0,1)を解析結果から抜き取りRate of Twist(θ)を計算します。
材料定数はYoung Modulus=69.×106[Pa], Poisson's Ratio=0.3です。
この場合Shear Modulusは26538461.5384615[Pa]になります
３次元の弾性解析では8-noded-1次ヘキサ要素と27-noded-2次ヘキサ要素でシャフトの要素分割を行っています。
分割数はx方向が20、yとz方向が4です。
下図は27-noded-2次ヘキサ要素を用いた時のFree Endの状況を示します。
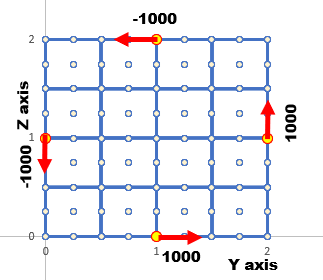赤色の矢印が力を示します。
各力のArm lengthが1[m]ですので、モーメント(M)は合計でM=4000[Nm]になります。
8-noded-1次ヘキサ要素の場合のFree endの状況は以下になります。
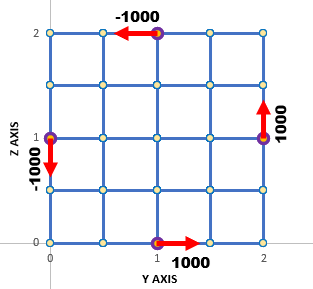
解析とポスト処理が終了するとRate of Twist(θ)の結果はファイルANGLE.DATへ書き込火れます。
Angle of Twist(β=xθ)とRate of Twist(θ)は以下で計算しています。
\begin{eqnarray}
\beta (x)=arctan\left(\frac{v\left(x,0,1\right)}{1}\right)
\end{eqnarray}
\begin{eqnarray}
Rate\ of\ Twist\left(\theta\right)=\frac{\partial\beta (x)}{\partial x}=\frac{\partial\left(x\theta\right)}{\partial x}
\end{eqnarray}
下図に変位v(x,0,1)、Angle of Twist、Arm length(長さ=1)を示します。
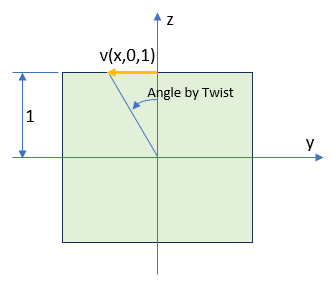先へ進む前に再度Torsionの解析で出てくる定数および未知数を以下にまとめておきました。
使っているシンボルは文献により異なります。
- G=Shear Modulus [Pa]
- β(x)=ねじれ角=シャフトの回転角(Angle of Twist または単に Twist)
- θ=単位長さ当たりのシャフトの回転角(Rate of Twist)
- Mx=シャフト端部x軸周りでのモーメント [Nm]
下図は例として2次ヘキサ要素を使って得られた、v(x,0,1) vs. xです。
Saint Venant theoryのところでは、シャフトの長手方向の座標がzでしたが、ここでは座標xを使っています。
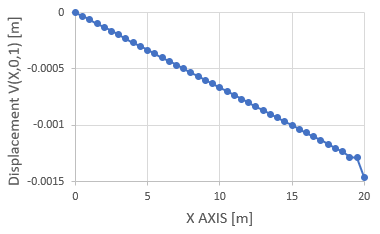そしてAngle of Twist(or Twist)を計算すると以下のTwist vs. x が得られます。
最後に下が Rate of Twist(θ) vs. xのグラフです。
Rate of Twist(θ)は単位長さ当たりのねじれ転角ですから、上のグラフの勾配にあたいします。
右端と左端でθの乱れは有りますが、殆どの領域で一定値に成っています。
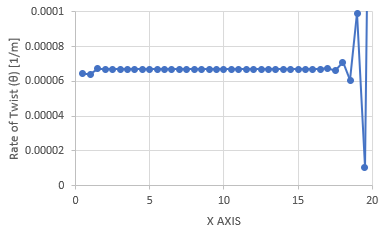
計算結果からθ=0.0000670055862315403が得られました。この値は要素数を次第に増やしていって収束した値です。
解析プログラムとデータ作成プログラムおよび描画データ作成プログラムしては、以下を使いました。27-Nodedヘキサ要素で3次元弾性解析を行うと、Globle Stiffness Matrix [K]が大きくなりPCが息をつくようになります。でのその間にコーヒーでも飲んでいると計算は終わります。なんとかしてMulti-CPUで計算できるようにプログラムを改善したいと思います。
計算条件が揃ったので3次元弾性解析ソフトを1次ヘキサ(8節点)と2次ヘキサ要素(27節点)で実行してみました。以下が得られました。
要素分割数は上でも述べましたが、x方向が20、yとz方向が4です。
| E [Pa] | ν | G [Pa] | 要素 | M[Nm] | θ [Radian] |
|---|
| 69×106 | 0.3 | 26538461.5 | 1次ヘキサ | 4000 | 0.000063686 |
| 69×106 | 0.3 | 26538461.5 | 2次ヘキサ | 4000 | 0.000066933 |
上表を見ると、1次要素の方が2次要素に比べRate of Twist(θ)は小さいですね。
これは1次要素のShear Lockingが影響していると思われる。
今回の解析ではせん断応力のみが発生していますので、Shear Lockingを起こしやすい線形要素を使うとRate of Twist(θ)が小さくでます。
そこでShear Lockingがほぼ無い2次ヘキサ要素(27節点)で分割する要素数を増やして計算を続行してみました。
シャフトの長手方向のX座標方向に要素を増やしてもθに影響しなかったのでNEX=20に固定し、NEYとNEZを2～8の間で計算してみました。
下のグラフは、横軸がシャフト断面の要素数です。縦軸がθです。
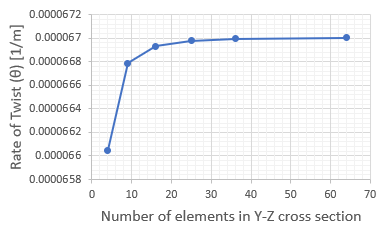NEY(8)×NEZ(8)=64でRate of Twist(θ)は収束しているようです。
そしてRate of Twist(θ)の収束値はθ=0.0000670055862315403でした。
このθは上で紹介した
POST3DTAUX-WITH-TORSION-PROBLEM.FOR
が計算してくれます。結果はファイル
ANGLE.DAT出力されます。このファイルをエクセルに読み込ますと、一番右の列にRATE-OF-TWISTが有ります。
ここを見ると、θ=0.0000670055862315403のなっていることに気付くと思います。
このθとNEX＝NEY=10を使ってtorsion9q.forを実行してみました。
1/4モデルでM=999.9 [Nm]でしたので、フルモデル換算でM=3,999.6[Nm]となり、3次元弾性解析の入力値のM=4000[Nm]と整合性がとれています。
3次元弾性解析と2次元Torsion解析との比較ですが、
3次元弾性解析ではShear ModulusとシャフトのFree EndにモーメントM=4000[Nm]を与えることによりRate of Twistθ=0.0000670055862315403が得られました。そして2次元解析ではShear ModulusとRate of Twist(θ)を与えてモーメントM=3999.6[Nm]が算出されました。結果は良く一致しています。
| 項目 | 3次元弾性解析 | 2次元解析 |
|---|
| 与える数値 | Shear Modulus, モーメント | Shear Modulus, Rate of Twist(θ) |
| 得る数値 | Rate of Twist(θ) | モーメント |
■3次元弾性解析による反り(Warping)について■
Torsionの理論のところで反り(Warping)について触れました。2次元Torsion解析でこの反りを計算できるかどうかは今後考えるとして、
3次元弾性解析結果からこの反りを拾うことが出来ます。以下は、x=10[m]の位置(シャフトの中央)でx方向の変位u(10,y,z)をエクセルの等高線でプロットした結果です。
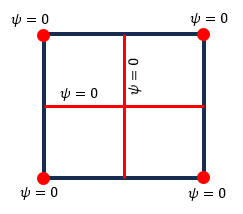
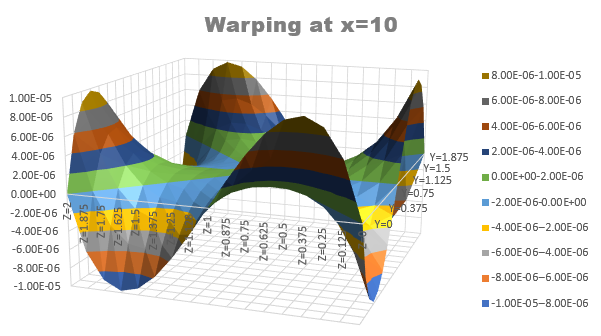このグラフの元データを見るとシャフトの四隅で反りがゼロになっています。また、下図に示す赤色の線上でも反りはゼロになっています。
Theory of Elasticity, Timoshenkoに有る実験結果と一致しています。
この結果は2次元の反り解析でDirichlet型境界条件として使えそうですね。
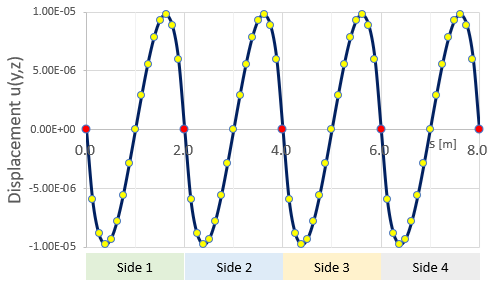
ちなみにシャフトの壁沿いに反りであるDispalcement u(y,z)をプロットしてみました。赤色の点がシャフト断面の四隅です。反り形状はシャフトの断面の各辺で同じです。理屈通りの結果になっています。
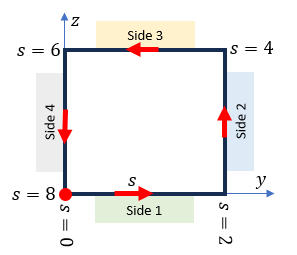
上のグラフの横軸ですが、下図に示す様にシャフト断面の壁沿いを進む路線が座標 s です。一周で8mあります。図の左下の赤丸の点が座標 s の出発点と終着点です。
計算結果の変形を図化してみました。下図に示す変位量は、計算された(u, v, w)に大きな値を掛けてMagnifyしてあります。まず、下図はTop-Viewです。赤の矢印はモーメントを与えるための力です。
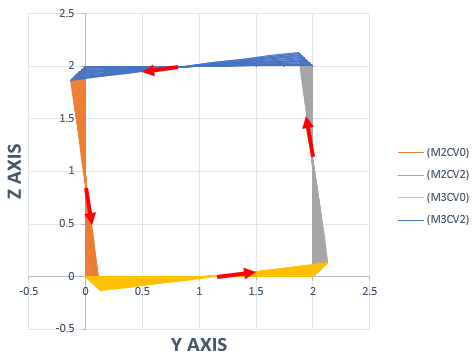下図は、Side-Viewです。変形はx-z 面から透かして見た図に成っています。反りの状態が解ると思います。下図を見ると、Shaftの四隅の長手方向の変位量はゼロになっているのが分かります。
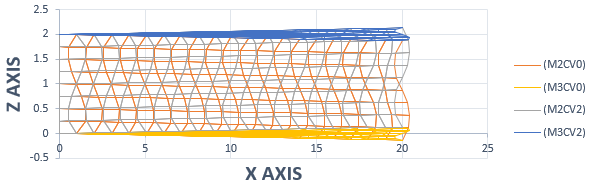この四隅の長手方向の変位量がゼロ(Dirichlet境界条件)という結果を用いて、反り解析をBEMで行いたいと考えています。
■3次元弾性解析による応力について■
応力もx=10[m]の位置で描画してみました。これも反りと同様にエクセルの等高線を使いました。以下にτxyとτxzを示します。
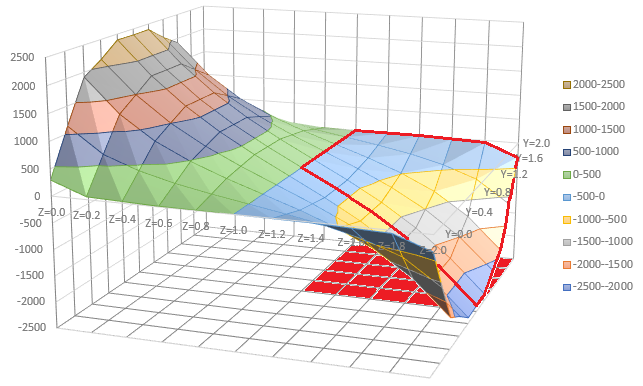
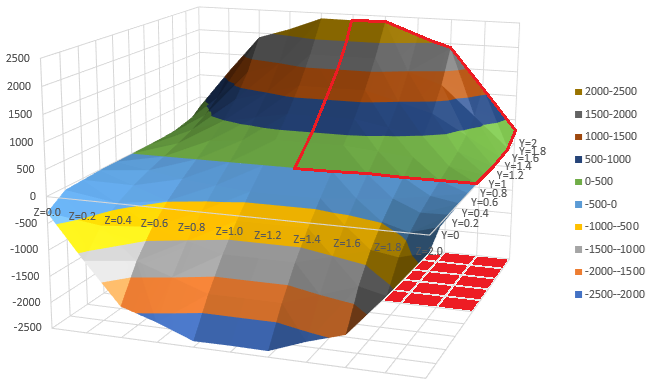図中の赤線で囲った部分は2次元解析ので使った計算領域です。2次元解析と3次元弾性解析の応力は良く一致しています。
これでTorsionに関しての3次元弾性解析は終了です。
Menu
Theory-Torsion
FEM-Torsion
BEM-Torsion
3DIM-Torsion
Internet College of Finite Element Method