Numerical Method & Algebla
Matrix-5
展開を進めると、以下の様になります。

上の関係式は、有限要素法での式の展開で頻繁にでてきますので、今の内に上の関係式が正しいことを、しっかり勉強しておいて下さい。
では、1次元の場合、どうなるのでしょうか。下は、1次元1次要素の近似式です。
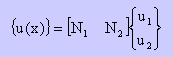

N1とN2は、形状関数と呼ばれています。節点でのu1とu2は、上の図に示す通りです。
ショートハンドノーテーションでは、{u(x)}=[N]{u}と書けます。
[N]を形状マトリックスとでも呼びましょうか。ベクトル{u}は、2つのコンポーネントを持っていますが、{u(x)}は1つです。
つまり、ベクトル{u}のコンポーネント数は、要素の節点数に依存し、{u(x)}は未知関数の数に依存していることに成ります。
ちょっと頭がくしゃくしゃしてきましたね。
まー、雰囲気がつかめればOKです。
では du/dxとdδu/dxは、どの様に書けるのでしょうか。
以下の様になりますね。
左辺は、コンポーネント数が1のベクトル数です。
この場合ベクトルのコンポーネント数は、式の次元に関係してきます。
 ショートハンドノーテーションでは、{du(x)/dx}=[B]{u}です。
形状マトリックスの微分を[B] マトリックスと呼びます。
すると(du/dx)と(dδu/dx)の積は以下の様になります。
ショートハンドノーテーションでは、{du(x)/dx}=[B]{u}です。
形状マトリックスの微分を[B] マトリックスと呼びます。
すると(du/dx)と(dδu/dx)の積は以下の様になります。
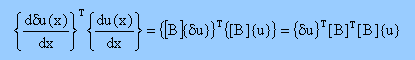 2次元の時と同じ形になりましたね。
有限要素法では上式の様に視覚的に覚え易いマトリックス演算式を生成します。
1次元では、Matrixの表記法にこだわったため{u(x)}=[N]{u}の様に書きました。
右辺の{u}は、節点でのu(x)の値を示します。左辺の{u(x)}は、微分方程式中の未知数(unknown)の数や式の次元数に関係しています。
つまり、コンポーネント数=1です。コンポーネント数=1なのにベクトル表示するのは
誤解を招きかねないので1次元の問題および変数の表現に限って以下の表記方法を使うことにします。
2次元の時と同じ形になりましたね。
有限要素法では上式の様に視覚的に覚え易いマトリックス演算式を生成します。
1次元では、Matrixの表記法にこだわったため{u(x)}=[N]{u}の様に書きました。
右辺の{u}は、節点でのu(x)の値を示します。左辺の{u(x)}は、微分方程式中の未知数(unknown)の数や式の次元数に関係しています。
つまり、コンポーネント数=1です。コンポーネント数=1なのにベクトル表示するのは
誤解を招きかねないので1次元の問題および変数の表現に限って以下の表記方法を使うことにします。
 次は、連立方程式の解き方です。
次は、連立方程式の解き方です。
 内容について疑問および質問がある場合は、左のQ&Aボタンを押して下さい。
内容について疑問および質問がある場合は、左のQ&Aボタンを押して下さい。
BACK
NEXT Simultaneous
Menu
Integral
Derivative
Matrix
Simultaneous
Internet College of Finite Element Method


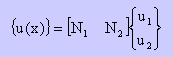


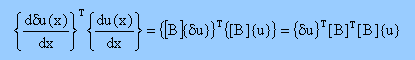

 内容について疑問および質問がある場合は、左のQ&Aボタンを押して下さい。
内容について疑問および質問がある場合は、左のQ&Aボタンを押して下さい。