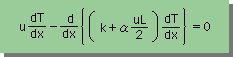
Added viscosityは、dxをL で置き換えたたために起きた不都合を修正する必要不可欠な パラメーターであると言えます。つまり、数値解析では、 下の微分方程式を解くと、安定し且つ精度の高い数値解がえられることになります。
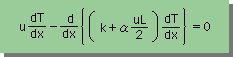
■差分でのUpwind method■
もともとUpwind method は、差分法の分野で開発されました。差分法では、1階微分を3つの方法で表すことが出来ます。
| Type | 式 |
|---|---|
| Forward difference | ΔT=(Ti+1-Ti)/L |
| Backward difference | ∇T=(Ti-Ti-1)/L |
| Central difference | δT=(Ti+1-Ti-1)/(2L) |
当初、差分法では、1階微分項の処理に、風上差分が使われていました。風上差分とは、速度(u)の方向をチェックして1階微分の近似方法を定めていました。例えば、u がx 軸のプラスの方向を向いていると、Backward difference を使い、その逆であるとForward difference を使います。この方法だと、速度(u)の方向を判定するというステップが必要になります。
ところが、1階微分項を下式の様に近似すると、その判定が不要になるばかりか、α=1または0以外の値も使うことができる。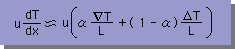
■流体解析への応用■
ここで紹介したUpwind methodをアップリケーションプログラムへ応用するとなると、様々な問題に遭遇します。私は、2次元の熱解析をカップルした流体解析に4-noded isoparametric 要素を使っています。この要素は、座標軸方向に限って1次要素に近い性質を持っているため、私はここで紹介した Added viscosity を使っています。
計算手順としては、t+Δt 時のAdded viscosity を得るために、各要素毎にt時の速度ベクトル{|u|,|v|}の最大値umaxとvmaxを計算します。要素の長さもLxとLyを前もって用意しておきます。すると、x方向とy方向のAdded viscosity は次の様になります。
| k'x=k(1+γxα(γx)) | γx=umaxLx/(2k) |
| k'y=k(1+γyα(γy)) | γy=vmaxLy/(2k) |
時間的に、Δt遅れの情報でAdded viscosity を計算していますが、安定した解析が得られています。次のテーマのFluid Dynamics で、Upwind Methodの計算例を紹介しています。