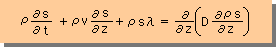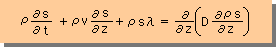
時間微分項と移流項の処理方法の実際を学んで頂くために、 1次元のConvection- Diffusion Equationの有限要素法を紹介します。 紹介するといっても、処理方法の詳細は、既に学習しましたので、ここでは、扱う微分方程式と計算結果を紹介をします。
■Inverse Problem■
1次元でも、Convection- Diffusion Equationを解くことにより、様々な物理現象をコンピューター上で再現できます。
| 湖底からコアーサンプルを抜き取ります。 |
| コアーサンプルを数ミリ間隔に切断します。 |
| 各切断されサンプルに対し、土の密度と観測したい物質の放射性同位元素の質量の濃度(dpm/gram)を測定します。 |
| 過去の活動が正確に知られている物質(Cs-137等)を用い、湖底に体積する年間の土の量(r=Sedimentation rate)を推測します。この推測には、Convection- Diffusion Equationをv(x,t)=r(t)/ρ(x)で解く必要があります。 |
| 初期条件を推定します。つまり、数十年前の湖底の土における、物質の深さ方向の濃度のことです。 |
| Convection- Diffusion EquationからNeumann型境界条件を未知数とした連立方程式を立てます。Nuemann型境界条件とは、湖底の水とsediment(土)との境における物質のfluxを意味します。 |
| 連立方程式を解くと、地球上の物質に関する過去の活動を知ることができます。 |
■Convection-Diffusion Equationの有限要素法■
Inverse Problemの詳細には、文献を参照して頂くとして、ここでは、上の解析のベースになっている、Convection-Diffusion Equationを有限要素法で解く方法を紹介します。まず、ここで取り上げる微分方程式は、下に示す様な形をしています。