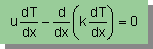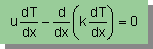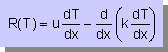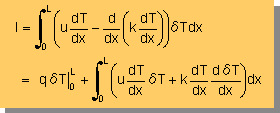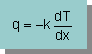数値計算を長年やっていて、最後まで私を悩ましたのが、1階微分の離散化です。 ここで紹介するUpwind method も完璧な方法ではありませんが、一応、問題は解決してくれます。

■Conventional Approach■
ここで取り上げる微分方程式としては、以前紹介した下式を使います。Upwind method の概念を 説明するには、1次元の微分方程式で十分です。

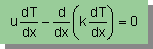上の式によると、熱は熱伝導係数(k)だけでなく、 流体の速度(u)によっても運ばれることになります。 この速度(u)が熱伝導による拡散速度よりも速い時に、 数値解析で問題を引き起こすのです。 この問題を披露してから、Upwind method を紹介します。 まずは、有限要素式を導くところから始めましょう。 その前に、上式のGeneral solution は、次の様になります。貴方は、General solutionが正しいかどうかを チェックして下さいね。

ここに、C₁とC₂は、境界条件によって決められる定数です。

そして、上の微分方程式の残差は、次の様になります。残差とは、上の微分方程式のT(x)に 近似解を代入したときに、下式のR(T)に入る値でしたね。

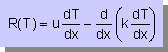さらに、積分式は、残差に重み関数をかけて、0 から L まで積分してゼロと置くことにより、 得られんでしたね。すると、次の様になります。Lは、要素の長さを意味します。

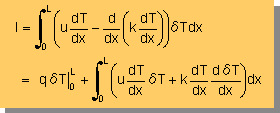ここに、q は下に示す様に heat flux になっています。

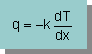さらに、1次要素で上の積分式を近似すると、 マトリックス型有限要素式は、次に様になります。