上の式は、理解できましたでしょうか。次は、上の式を一定要素 (constant element) 用に書き換えます。

■Constant Element■
Constant element とは、どの様な特徴を持っているかチェックしてみましょう。 まず下の図を見て下さい。

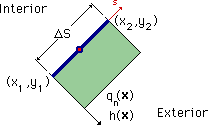
この要素上において、変数 h(x) 及び q_n(x) は一定になっています。要素の中央にある節点でそれらの変数が計算および指定されます。 例えば、h(x)が既知の場合、h(x)がその節点で指定され、そしてq_n(x) が計算されます。 q_n(x) が既知の場合は、h(x)が計算されます。 つまり、その節点が要素上の変数 h(x) 及び q_n(x) を代表しているということです。

変数が要素上で一定ということになると、積分式は、下に示す様にかなりシンプルになります。 つまり変数 h(x) 及び q_n(x) は、線積分の外に置くことが出来ます。