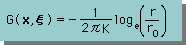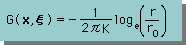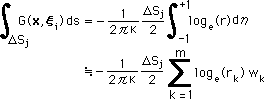Two Dimensional Boundary Element Method
Discretization by Constant Element-7
■Gijの計算■
やっと数値積分が出来るようになりました。手始めにGijをGauss 積分法で計算してみましょう。
Gauss-Legedre 積分法の使い方については、有限要素法でしっかりと勉強しましたので、ここでは行いません。
積分の前に再度Kernel Function を下に表示します。
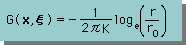すると、Gij の積分は、下の様に近似できます。
Index (添え字) i, j, k には、十分注意して、下式を観察して下さい。
また、上式の r0は、 r0=1 とし、今後の式の展開では記述を簡略化するためにr/r0=r とします。
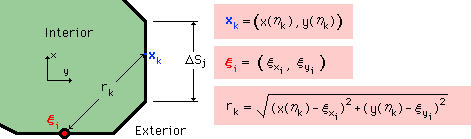
ここに、ξi は、Source point の位置を示します。
ΔSj は、積分が行われている要素です。
そして、r はΔSj 上の点(xk)とSource point 間の距離を示します。
ξi、ΔSj 、rk については、下図を参考にして下さい。
Source point を含む要素上の積分については、後程取り上げます。
BACK
NEXT
Menu
Fundamentals
Formulation
discretizatione
Example
Straight
Multi-D
