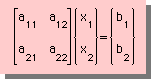 |
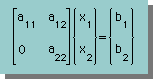 |
■Gaussの消去法■
ではGaussの消去法のアルゴリズムは、どの様かを見てみましょう。
早速下の左に示す2X2のマトリックスをもつ連立方程式をGaussの消去法で解いてみよう。
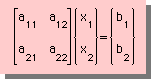 |
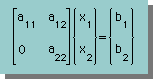 |
ここで、もし上式のa21=0 だった場合つまり上右図の状態の時です。 2行目の式より、x2=b2/a22ですから、 x1=(b1-a12x2)/a11となる。 連立方程式の解が、得られたことになります。 ここに、x2とx1が成立する条件としてa11とa22がゼロであってはなりません。
問題に戻って。 どうすればa21=0にすることができるかです。 まず、連立方程式を取り扱う上で2つのルールを紹介しておきます。
| 連立方程式の何れの式にゼロ以外の実数を乗じてもよい。 |
| 連立方程式の何れの式を別の式に足し込んでもよい。 |
問題に戻って。 マトリックス型の式を次の様に書き改めます。
| a11 | x1 | + | a12 | x2 | = | b1 | .....Eq.1 |
|---|---|---|---|---|---|---|---|
| a21 | x1 | + | a22 | x2 | = | b2 | .....Eq.2 |
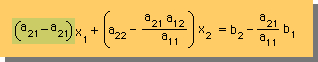
| x2= (b2-b1a21/a11)/(a22-a21a12/a11) |