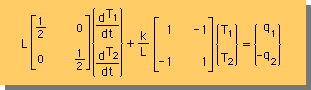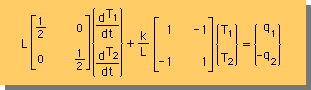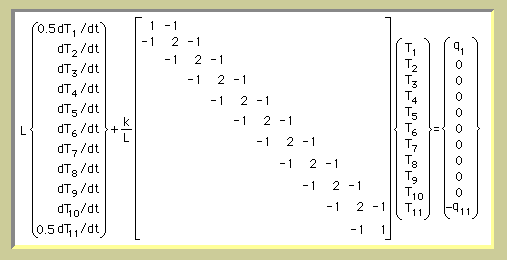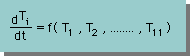Time Derivative and Upwind Method
Time Derivative Term-2
次は、マトリックス型積分式のIを{δT}で微分して、=0 とおきます。
これは、通常のWRMの手続きですね。
すると、次の有限要素式が得られます。
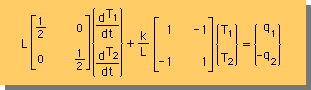 練習のために、計算領域を、長さLの1次要素で10等分したときの、Globalの連立方程式を作ってみましょう。
つまり、上式をGlobalマトリックスにAssemblyするということです。次の様になります。
練習のために、計算領域を、長さLの1次要素で10等分したときの、Globalの連立方程式を作ってみましょう。
つまり、上式をGlobalマトリックスにAssemblyするということです。次の様になります。
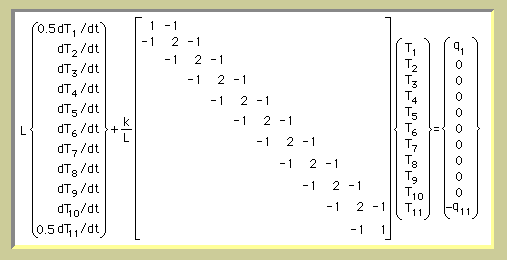 上の式は、x座標に無関係になっています。
つまり、時間(t)だけに依存している連立常微分方程式であることに気付いたと思います。
したがって、下の常微分方程式が解ければ、問題は解決することになります。
上の式は、x座標に無関係になっています。
つまり、時間(t)だけに依存している連立常微分方程式であることに気付いたと思います。
したがって、下の常微分方程式が解ければ、問題は解決することになります。
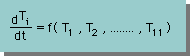 この常微分方程式を数値的に解く方法には、Runge-Kutta方法をはじめとし、様々方法が提案されています。
しかし、何れも連立常微分方程式を解くには不向きな方法です。
理由として、(1)掛け算と割り算の回数が多い、(2)安定性が悪い、(3)プログラムが複雑になる、等が上げられます。
この常微分方程式を数値的に解く方法には、Runge-Kutta方法をはじめとし、様々方法が提案されています。
しかし、何れも連立常微分方程式を解くには不向きな方法です。
理由として、(1)掛け算と割り算の回数が多い、(2)安定性が悪い、(3)プログラムが複雑になる、等が上げられます。
ただ利点といえば、精度が良いということです。
しかし、時間軸方向だけ精度が良くても、x方法の精度(1次要素)が悪ければ、全体の精度は上がりません。
ですから、精度は、まーそこそこで、演算回数が少なくて、安定性の良い方法を選ぶのが最適と言えますね。
BACK
NEXT
Menu
Heat Equation
Time derivative
Upwind
1 Dim Example