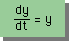
■First Order ODE■
そこで、ここでは下の最もシンプルな常微分方程式を解く、3つの数値計算方法を紹介します。
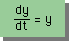
時間 t が 0 から Δt 進んだ時点を考えみましょう。すると、Exact solution では次の様に書き表すことが出来ます。
| y(t)/y(0) = 1 + Δt + (1/2)Δt2 + (1/6)Δt3 + ............ |
■時間項の近似■
近似解ではどうなるか。まず、時間項は下に示す式で近似します。これは、最も簡単な差分の式です。有限要素法では、時間項処理に差分法の力を借りることになります。
| 時間項処理手続き その2 |
|---|
時間項は 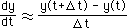 で近似する。 で近似する。 |
■CASE 1 : Explicit Method■
その第1の方法として、Explicit Method を紹介します。
この方法は、微分方程式の右辺のyを時間t=tの値と考えます。つまり、下式です。
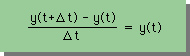
| y(t+Δt)/y(t) = 1 + Δt |