| Method | T2(t+Δt) の式 | T2(t+Δt) at Δt=∞ |
|---|---|---|
| Explicit | 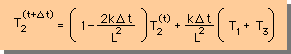 |
-∞ |
| Implicit | 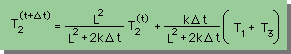 |
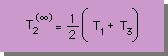 |
| Crank- Nicolson |
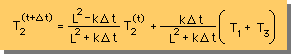 |
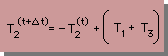 |
■3 Methods のまとめ■
下表に、3つの方法による T2(t+Δt) の式と、Δtが無限大に近いときの T2 の式を示します。
| Method | T2(t+Δt) の式 | T2(t+Δt) at Δt=∞ |
|---|---|---|
| Explicit | 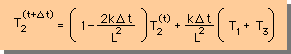 |
-∞ |
| Implicit | 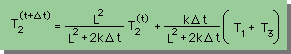 |
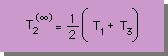 |
| Crank- Nicolson |
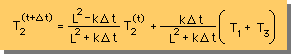 |
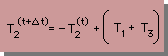 |
■例題■
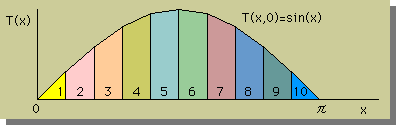
例題を計算し、いままで説明したことを復習してみましょう。下図に示す様に、領域として、長さπを考慮します。それを10等分します。つまり、要素の長さが、π/10 になります。スペースの従属変数(x)と時間の従属変数(t)は、無次元化されているものとします。そして、初期値は、T(x,0)=sin(x) です。
■プログラムHEAT1DIM.FOR■
時間項の数値計算の学習をスムースに行うために、インタラクティブなプログラムHEAT1DIM.FORを作成しました。
このプログラムを実行すると、解析に必要な項目を、キーボードから入力出来る様に設計されています。
入力項目に様々な値を入力して、Explicit method, Implicit method, Crank-Nicolson metod の特徴を勉強して下さい。
なお、領域、初期条件、境界条件は、上の例題と同じです。