Electromagnetics and Ham Radio
Inductance2
ではどのような手順をふめば磁束密度
B
、が計算できるのかです。
また閉ループC1はどの様に決めればよいのかが問題になります。
出来るだけ電気磁気学の書物等にのっとって計算方法を説明してゆきます。
また、自己インダクタンス(L)は、有限要素法でも境界要素法でも計算できますが電磁気の場合、
無限領域の問題が多いので、出来るだけ境界要素法で問題を解きます。
しかし、同軸ケーブルのような閉空間や複数の誘電率εと透磁率μがある場合は、有限要素法が便利です。
まずは微分方程式の導出から行います。
ここで使っている文字についてお知らせしておきます。
まず、アルファベットやギリシャ文字の太文字(bold letter)はベクトルを意味します。
例えば、
B, E, A, J, t, n
などです。また、座標にも太文字を使うことが有ります。
例えば、f(x), u(ξ),
C(ξ)です。これも座標の点を意味するベクトルです。
これらは、二次元の場合、f(x,y), u(ξ,η), C(ξ,η)と同じ意味です。
■磁束密度Bと
磁気ベクトルポテンシャル(A)との関係■
磁束と電流Jに関して、定義として書物等に書いてあることは、真空中において電流で発生する磁束密度Bは、
次に上げる2つの式を満足するものでなければなりません。
divB=0
rotB=μ0J
磁界の発散は、常にゼロであることを示している。
静電荷の場合+の電荷を含む場では、
divE>0、‐の電荷を含む場では、divE<0、
電荷を含まない場では、divE=0となっています。
しかし、磁束密度Bの発散は、どんな場合でもゼロになっている。
仮に以下の式が満足するベクトルAがあるとする。
そしてAの回転を磁束密度Bとします。
B=rotA
上式が成立するのであれば、Bの発散はゼロにならなければなりません。つまり、
divB=div(rotA)
ストークスの定理によると、上式は常に満足することになります。
このAのことをBの磁気ベクトルポテンシャルと言います。
以上のことから
B=rotA
とおくことで
divB=0
が満足されるので、最終的に解かなければならない式は、以下になる。
rot(rotA)=μ0J
ちょっと複雑な式が残りましたが、上式の左辺を展開すると以下になります。
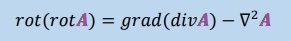ここで、divA=0が成り立てば問題は更に単純になります。つまり、
∇2A
=-μ0J
Preceding Page
Next Page
Menu
Inductance
Capacitance
Z0
Exp
Balun
Coaxial
Off center fed DP
Helmholtz
FEM
BEM
Internet College of Finite Element Method