■計算手順■
これで、プログラミングを行うための材料は、全て揃いました。といっても、いまだに計算手順がはっきりと理解しきれていない貴方のために、Source pointの位置と積分結果が格納されるマトリックスを示します。

図中の赤い点が Source point です。この点から要素上の点までの長さが、Kernel function にある距離 r です。まず、 Source point が節点１に有ります。そして積分が実行されている要素は、 Source point がある要素番号1です。上図の場合、節点番号と要素番号は、同じになります。

要素番号1上で計算された F₁₁とG₁₁ の積分は、上図の着色された[F]と[G]へ格納されます。また、F₁₁は、着色された[C]へ加算されます。話は、スムーズに行く様に思えますが、ちょっとひっかかる点があります。それは、Source point を含む要素のG_ij の計算です。要素の端からもう1つ端に向かって積分していると、GがSource point で無限大になってしまいます。積分結果は有限値になりますから何の問題はありませんが、数値計算上で特別な取り計らいが必要です。それについては、後程詳しく紹介します。

次に、 Source point はそのまま節点１にある状態で、要素番号2上を積分している状態を下図に示します。

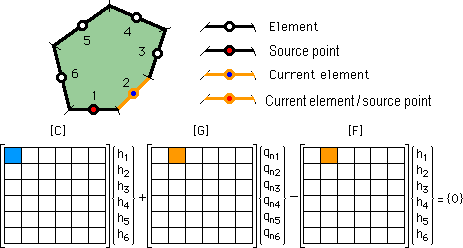FとGの積分結果は、マトリックス[F]と[G]のF₁₂とG₁₂ へ格納されます。そして、F₁₂をC₁₁に加算されます。この操作を要素番号6まで行います。すると、[F]と[G]の1行が全て埋まることになります。さらに、C₁₁の計算を終了します。

今度は、Source point を要素2へ移した状態を説明します。下図を見て下さい。要素番号1上を積分している状態を示しています。

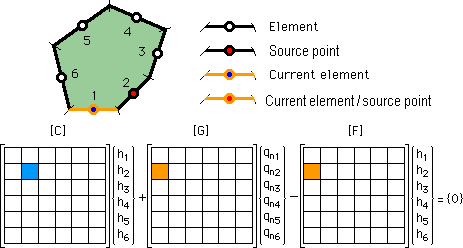FとGの積分結果は、マトリックス[F]と[G]のF₂₁とG₂₁ へ格納されます。そして、F₂₁は、C₂₂に加算されます。これらの操作を全ての要素上で行うと、マトリックス式の第2行が完成します。
後は、Source point を要素3,4,5,6へ移して同じ操作を行えば良いのです。何となく計算の進め方は理解できましたか。次は、実際にFとGの積分のやりかたを説明します。