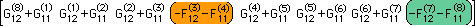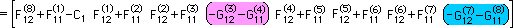Parametric Representation of Boundary Elements in 2Dim
Corner Problems-6
次に、上の式を未知と既知に分けます。下式がそうです。
全てのSource point について上と同様な計算を実行すると、[A]{X}={RHS} の連立方程式になります。つまり、上式の左辺(上段)のベクトルが、未知の{X}です。そして、右辺は、既知です。この例題の場合、未知は、q1、q2、q3、h4、q5、q6、q7、h8 ということになります。本当の未知は、線形要素で紹介した8つです。
上で起きている事柄をまとめると、以下のことが言えます。
|
従来の方法は、[C]{h}+[G]{q}-[F]{h}={0} を生成する過程で、qn を歪曲(わいきょく)させてしましい、既知の qn を正しく再現していない。
|
ここでは、2つの Corner problems の対処方法を紹介しました。そして、ここで学習した事柄をまとめると、以下の様になります。以下の事柄は、線形および高次の要素に適応されます。また、ここで紹介した方法の類似法については、文献を参考にして下さい。
| 節点での内角が180度から大きく離れている場合、その節点を、隣接した2つの節点で置き換える。その節点の前後の要素が、Dirichlet 型境界条件の時に効果を発揮する。 |
| 要素毎の積分を行いながら、連立方程式 [A]{X}={RHS} を直接、生成する。 |
次に、有限要素法のh(x,y) と qn を真似た、mixed form 法を紹介します。h(x,y) を線形要素で、 qn を一定要素で表します。つまり、究極のCorner problems の対処方法といえます。有限要素法では、h(x,y)をn次で近似した場合、qnは、n-1次で近似されます。
