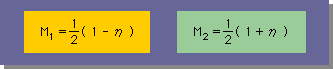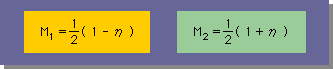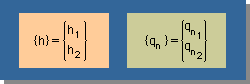Parametric Representation of Boundary Elements in 2Dim
Linear Element
■1次要素の形状関数と近似式■
2次元の境界要素法で使う1次要素は、1次元の有限要素法の1次要素と同じです。
また、積分に Gauss-Legendre 法が使える様にするために、有限要素法と同様に、形状関数を無次元座標系で書きます。
したがって、1次要素では、境界上の h(x) と qn(x) を表す形状関数は、次の様になります。
(参考: x=(x,y) のことです。)
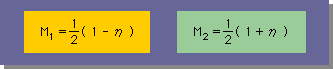有限要素法と歩調を合わすため、形状関数にMを使うことにします。
すると、 h(x) と qn(x) は、次の様に近似できます。
ここに、[M]=[M1 M2] です。{h} と {qn} は次の様に定義します。
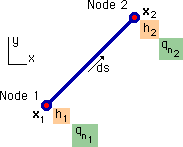
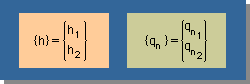つまり、h1 は、下図に示す節点1(Node 1) での h(x) で、h2 は節点2(Node 2) での h(x) です。
{qn} にも同様なことが言えます。
BACK
NEXT
Menu
Linear
Corner
Mixedform
Parabolic
Example
